z

Le distanze cosmologiche: l’epopea degli Herschel ( in fase di costruzione … )

Z

i fratelli Herschel: il catalogo delle Stelle Doppie

Z

William si era proposto di misurare lo spostamento parallattico di una stella rispetto ad una vicina, che cadesse nel campo visivo dello strumento, al fine di rendere più precisa e facile la misura. Ma la realtà dell’osservato andava dicendo che nella massima parte di casi le stelle scelte sembravano gravitazionalmente legate, e quindi alla stessa distanza, vanificando l’idea di misurare una parallasse differenziale.

Egli scoprì, pertanto, degli effettivi sistemi binari e non stelle doppie visuali. Non sarà lui a misurare la prima parallasse annuale.

Fu così che nel tempo venne pronto un ampio catalogo di stelle doppie, realizzato in tanti anni di assiduità “al pezzo” e con l’insostituibile contributo della sorella Caroline

Egli, da sempre, aveva avuto la smania di realizzare, su suo stesso progetto, strumenti sempre più grandi. Fu così che si trovò a disporre di una grande varietà di telescopi con differenti diametri dello specchio. Ciò gli permise di misurare, in modo relativo, le distanze di molte stelle, assumendo ipotesi semplificative davvero strabilianti, ad alto rischio se vogliamo, ma necessarie per fare i primi passi verso nuove conquiste.

L’ipotesi era che le stelle misurate avessero tutte la stessa magnitudine assoluta. Questa grossolana assunzione permise a Herschel di disegnare la forma della Via Lattea, la nostra galassia, le cui stelle sono quelle che comunemente vediamo in una notte stellata.

Z

i fratelli Herschel: la Galassia è grande e il Sole è al centro

z

 Z

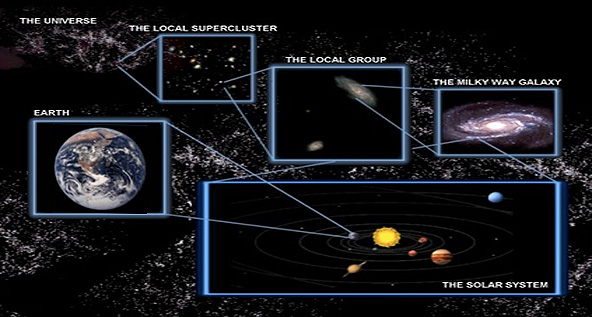
i fratelli Herschel: la Terra e il Sistema Solare stesso sono un bruscolo all’interno della Galassia

z

« Il Sistema Solare, il regno del nostro Sole è un angusto cortile, da confrontare con la vasta metropoli della Via Lattea. Dopo Herschel, gli scienziati dovranno porsi il problema di spiegare come si sono formati gli universi-isole, come si distribuiscono nello spazio, quanto è grande l’Universo che li contiene. È l’atto della nascita della moderna cosmologia. » (1)

Z

Friedrich Wilhem Bessel: la misura della Prima Parallasse Annua

z

Z

Henrietta Swan Leavitt: le 16 Cefeidi nella Piccola Nube di Magellano

z

Z

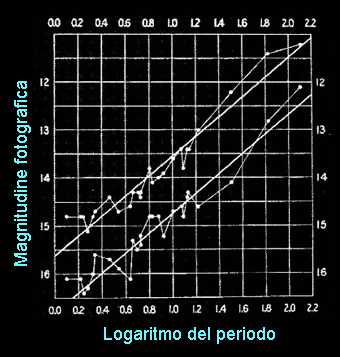
Henrietta Swan Leavitt: la relazione Luminosità-Periodo ( L-P ) delle Cefeidi

z

Z

Harlow Shapley: la Via Lattea è enorme, comprende tutto l’osservabile, il Sole è in periferia

z

Z

Edwin Hubble & Milton Humason al telescopio di Mt.Wilson

Z

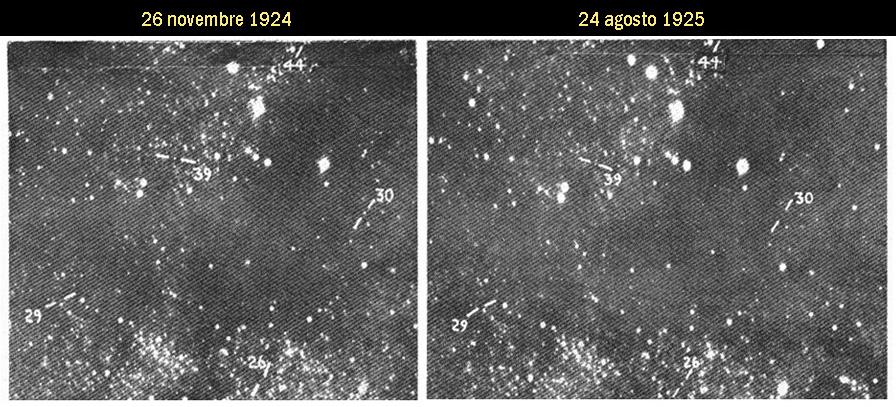
Edwin Hubble scopre le Cefeidi in M31 ( Galassia di Andromeda )

z

Variazioni cospicue in 26, 30. La stella 44 è una variabile irregolare. Poca variazione in 29, 39.  ( Edwin Hubble – “The realm of the Nebulae” - 1936 )

Z

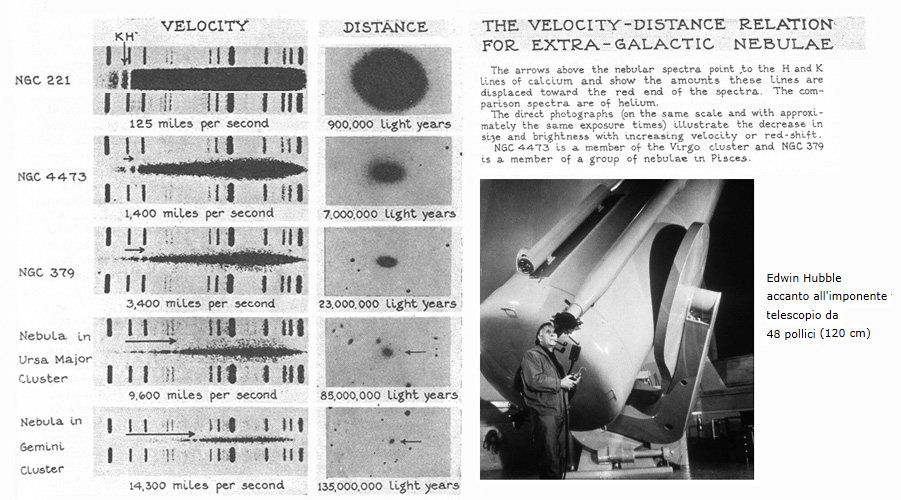
Edwin Hubble scopre l’Espansione dell’Universo ( tramite il Redshift )

z

Con questa pagina, di una evidenza didattica immediata, Hubble entra nel mito.  ( Edwin Hubble – “The realm of the Nebulae” - 1936 )

Z

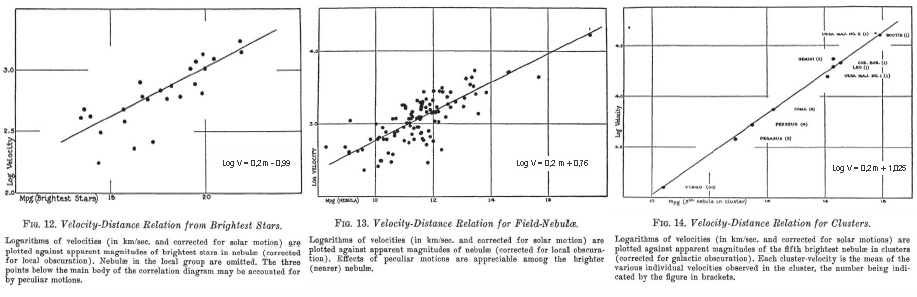
Edwin Hubble scrive la relazione Velocità-Magnitudine ( Velocità-Distanza )

z

z

Per tre “oggetti” Hubble ricava la relazione Velocità-Magnitudine apparente.  ( Edwin Hubble – “The realm of the Nebulae” - 1936 )

Misure contemporanee dello stesso tipo mostrano una dispersione assai minore, confermando, a maggior ragione, Hubble.

Log ν = 0,2 m + 0,76 è la relazione per le Nebulæ, nel linguaggio di Hubble esse sono fondamentalmente le galassie.

z

Z

Edwin Hubble: la calibrazione della relazione Velocità-Distanza

z

« L’espressione per la distanza in anni-luce è                  log d = 0,2 ( m_c – M ) + 1,513

dove M è la magnitudine dell’oggetto la cui magnitudine apparente vale m_c . Pertanto, nel caso delle stelle più luminose, dove M = -6,35 ( valore determinabile tramite la relazione della Leavitt ), allora:

0,2 m_c = log d – 2,783                   [ m_c corretta per l’attenuazione delle polveri – d corretta per il moto del Sole ]

Sostituendo questo valore di 0,2 m_c nella correlazione sperimentale  log v = 0,2 m_c + 0,76  si ha:

log v = log d -3,98    risolvendo    v = 0,000105 d    e passando ai milioni di anni-luce:

v = 105 d      v espressa in “Miles US Statute” = 1,6093 km,   d in milioni di anni-luce

v = 169 d      v espressa in km/s,   d in milioni di anni-luce = 0,30679 milioni di pc

z                                                                         v = 550 d      v espressa in km/s,   d in milioni di pc   ( legge di Hubble )

L’apparente velocità di regressione della nebula è di 550 km/s per milione di parsec. » (2)

(1)   Corrado Lamberti, “Capire l’Universo – L’appassionante avventura della cosmologia”, Springer Verlag Italia, 2011

(2)   Edwin Hubble, “The realm of the Nebulae”, Oxford University Press, London, 1936

Festival della Scienza 2011 - Corrado Lamberti – Universo omogeneo e legge di Hubble

Corrado Lamberti, “Capire l’Universo – L’appassionante avventura della cosmologia”, Springer Verlag Italia, 2011