|
|
Brillanza del “cielo stellato”
( in fase di
costruzione … )
z
|
|
|
|
Il cielo è da sempre stato considerato “la finestra” verso
l’infinito. Al tempo dei nostri avi non c’erano luci che lo potessero
sminuire, come oggi succede quasi ovunque.
Una serata senza Luna, in mezzo ai monti, sdraiati su un prato,
offre uno spettacolo di una bellezza indimenticabile.
Le stelle non sono tutte uguali,
alcune ( poche ) sono molto luminose, molte meno intense e tantissime
appena percettibili. L’uomo antico, grande osservatore stupefatto di questa
meraviglia, si è fin da subito premurato di classificare le stelle per
luminosità e colore.
Nel suo immaginario le più luminose erano le prime, le più
importanti, e pertanto erano di 1a grandezza, le altre
di 2a, 3a e così via fino alla 6a
grandezza, quella che solo un occhio perfetto riesce a vedere. Così è successo che quelle di brillanza maggiore si trovano
associato il numero minore.
Era stato dunque coniato il concetto di “luminosità apparente”, quello che
oggi è stato quantificato in modo da poterlo inserire in una formula.
Image credit: La Stampa
|
|
|
Z
z
|
|
Brillanza delle singole “stelle”
|
|
|
|
Oggetto
|
Magnitudine apparente
|
Brillanza
W/m-2
|
|
Sole
|
-26,7
|
1,37٠103
|
|
Luna piena
|
-12,74
|
5,35٠10-3
|
|
Sirio A
|
-1,46
|
1,03٠10-7
|
|
Stella generica
|
-1
|
8,02٠10-8
|
|
“
|
0
|
3,19٠10-8
|
|
“
|
1
|
1,27٠10-8
|
|
“
|
2
|
5,05٠10-9
|
|
“
|
3
|
2,01٠10-9
|
|
“
|
4
|
7,98٠10-10
|
|
“
|
5
|
3,17٠10-10
|
|
“
|
6
|
1,26٠10-10
|
|
“
|
7
|
5,02٠10-11
|
|
“
|
8
|
2,00٠10-11
|
|
“
|
9
|
7,95٠10-12
|
Z
z
|
|
|
|
Una caratteristica importante è la “ Luminosità
di una stella = ( L ) ”, cioè la potenza
totale emessa, si misura in Watt oppure in multipli di
(
 = Luminosità del Sole ). Per
trovare la Luminosità di una stella basta conoscerne la Brillanza “b” ( W/m2
) e la Distanza “d” (.m.) dalla
Terra. Il tutto si relaziona secondo la formula seguente:
b = L / ( 4٠π٠d2 )
“b” si misura al telescopio col bolometro. Facile a
dire, in concreto, dato i bassissimi valori del flusso, una misura che richiede
strumentazioni complesse ( tra cui temperature bassissime per ridurre a
valori accettabili il rumore termico ). Riscriviamo la formula precedente
per una stella generica e per il Sole:
L = 4٠π٠d2٠b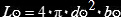 
dividendo membro a membro:
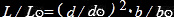
in questa relazione per trovare “L” basta
avere “d” e “b”, che come già visto possono essere determinati in qualche
modo.
|
|
|
Z
z
|
|
Magnitudine apparente, assoluta, Brillanza, Distanza
|
z
|
|
Questa è la relazione tra la magnitudine di
una stella e un’altra, in particolare ci si può riferire al Sole:
m1 – m2 = -2,5 log ( b1 / b2
) mSirio – mSole
= -2,5 log ( bSirio
/ bSole
)
Un salto di magnitudine equivale ad un
fattore 2,512 di
variazione nella Luminosità. Questo numero singolare soddisfa alla
seguente proprietà:
poiché 100,4
~ 2,5121886431….. allora 2,512 x 2,512 x 2,512 x 2,512 x 2,512 = ( 2,512 )5 ~
100
Un parametro significativo è la “ Magnitudine
assoluta M ”, definita come la brillantezza che avrebbe un oggetto posto
alla distanza di 10 pc. Si tratta di una distanza arbitraria, ma essendo
la stessa per tutte le stelle, ne quantifica di fatto la brillantezza
intrinseca. Vale la seguente utilissima relazione:
m – M =5 log d – 5
m = magnitudine apparente
M = magnitudine assoluta
d = distanza in parsec
|
|
|
|
|
|
Z
Luminosità assoluta di Arcturus e Sole ( a sinistra ) – Luminosità apparente ( al centro e a
destra )
z
|
|
|
|
Z
Dimensione di una stella
z
|
|
|
Questa è la relazione ( di Stefan-Boltamann ) che
permette di ricavare il raggio "R" di una
stella:
L = 4πR2
σ T4
L =
luminosità in Watt
R = raggio
della stella in Metri
σ = costante di Stefan-Boltzmann: 5,6 x 10-8 [ W m-2
K-4 ]
T =
temperatura della stella in Kelvin
|
|
Una stella
fredda ( bassa
temperatura superficiale ) potrebbe
tuttavia essere molto luminosa nel caso in cui avesse un grandissimo
raggio, dunque una immane superficie emittente.
Una stella
calda ( alta
temperatura superficiale ) potrebbe
tuttavia essere poco luminosa nel caso in cui avesse un piccolo raggio,
dunque una ridotta superficie emittente.
Ad esempio, Sirio A e Sirio B hanno circa la stessa temperatura [ ~10000 K ], ma un rapporto “ LA /LB ” pari a circa 6913 a favore di
Sirio A, più grande del Sole, mentre Sirio B ha dimensioni paragonabili a
quella della Terra. Si tratta di un sistema doppio
con periodo ~50 anni.
|
|
|
Z
z
|
|
|
Colore di una stella: la radiazione del “corpo nero”
|
|
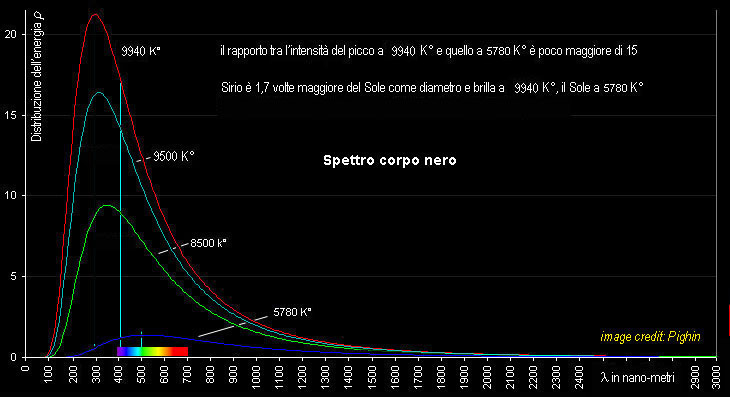
in prima approssimazione una stella
ha uno spettro simile a quello del "corpo
nero"
|
.
|
|
|
Colori
reali e apparenti di Sirio
e Sole
|
|
|
z
La legge
di Plank
afferma che la relazione tra la brillanza ( Energia /
superficie ) e le lunghezze d'onda che costituiscono lo spettro può essere
|
così rappresentata in
forma differenziale :
|
|
|
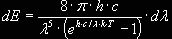
Imponendo che la
derivata di E( ) sia
nulla ( ciò accade nel punto di
massimo ), si ottiene la seguente
espressione:
|
|
|
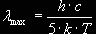
astro
|
raggio
in km
|
superficie
in kmq
|
T
in gradi K°
|
del picco
|
Colore dell'astro
|
|
Sole
|
696000
|
6,08735E+12
|
5780
|
498 nm
Verde
|
appare
all'occhio
Giallo
|
|
Sirio
|
1308500
|
2,15158E+13
|
9940
|
289 nm
Ultravioletto
|
appare
all'occhio
Bianco
|
Diventa evidente come ciò che appare all'occhio umano, che non vede tutte le frequenze con la stessa
sensibilità, ma è molto più sensibile ai colori caldi che non a quelli
blu e violetti, è diverso da ciò
che misurano strumenti a banda larga
...
è appunto per questo
motivo che il Sole appare giallo, pur avendo il picco di emissione nel verde ... Sirio appare nel cielo di un bianco splendente, ma ha il picco nell'ultravioletto ... anche
l'atmosfera filtra molto ... ecco perché è così importante avere
telescopi in orbita capaci di registrare lo spettro delle stelle ...
z
|
z
“Green Flash” - il Lampo Verde fuggente ...
z
image credit: Wikipedia dit: Wikipedia 
image credit: Wikipedia
“Green Flash” - il Lampo Verde fuggente ...
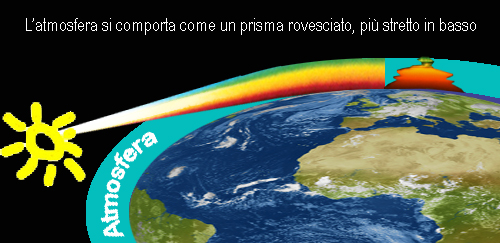
La ragione del lampo verde si trova nella
rifrazione della luce ( come in un prisma rovesciato ) a causa della atmosfera: i raggi del Sole seguono
percorsi leggermente curvi, come la superficie della Terra.
La luce ad alta frequenza ( verde / blu )
curva di più e pertanto può passare solo nella parte più alta, la luce a bassa frequenza
( rosso
/ arancio ) curva di meno e
pertanto può passare nella parte più bassa.
Allora i raggi verdi / blu
del Sole al tramonto vengono
separati dal "prisma
atmosfera" e possono diventare visibili
( i raggi rossi in quella zona, possono
essere addirittura ostruiti dalla superficie della Terra ).
|
|
|
“Costituenti” stellari
In costruzione …
z
|
|
|
“Spettri” e “spettroscopia” stellare
z
|
|
|
|
z
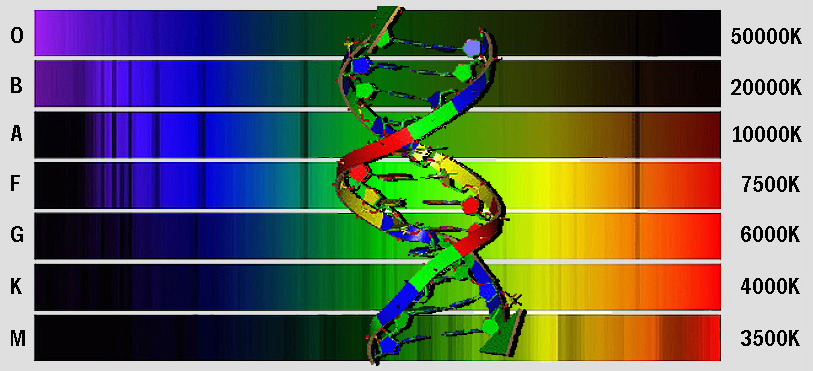
Lo spettro di una stella è la “ firma ” della
sua struttura: dà indicazioni sulla temperatura
superficiale, la distanza, la
direzione del moto, la rotazione e, per via indiretta, l’età, la massa, la vita futura … equivale
al nostro DNA che contiene le informazioni costitutive del corpo.
“Spectra” image credit: www.astroala.it - elaborazione pighin
|
|
Z
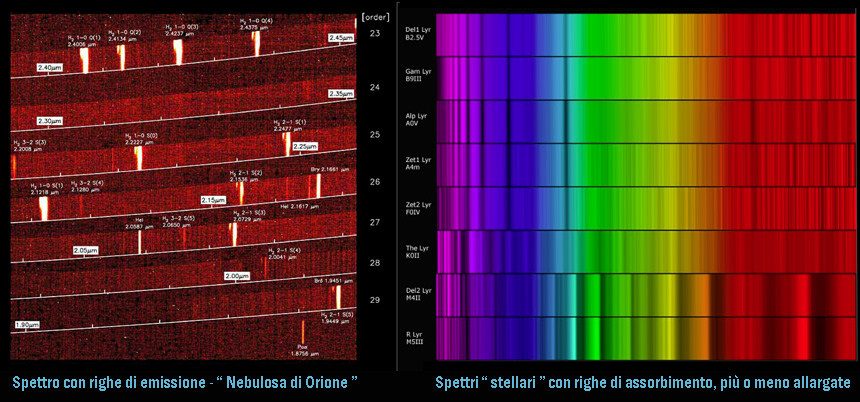
Due
tipologie fondamentali di “Spettri”: “nebule” e
“stelle”
zz
|
|
|
|
La parte rossiccia dello spettro delle nebulose è
fondamentalmente “ rumore di fondo ” … le nebule sono gas senza fusione
nucleare, ma fortemente eccitato … i costituenti della nebula lasciano la
loro firma sotto forma di righe di emissione
|
|
Z
“Spettri” e
“Spettroscopia”
z
|
|
« Le stelle
rosse hanno una grande quantità di luce che cade nella parte rossa dello
spettro e le stelle blu avranno una quantità corrispondentemente
maggiore di luce all’estremo blu. È ora importante notare che, oltre alla
luce dispersa, sarà presente una fitta serie di
righe scure sovrapposta a questo insieme di colori che ricorda un
arcobaleno.
Queste sono dette “ righe di assorbimento ”, e si formano nella atmosfera della
stella. In rari casi, ci sono anche delle righe brillanti, che sono dette
“.righe di emissione.”. È raro trovarle nelle stelle, mentre sono preminenti nelle
nebulose …
Quando
l’idrogeno gassoso viene riscaldato ad alte temperature, il numero di
collisioni tra atomi è così elevato che può continuamente “.pompare,” gli elettroni a livelli energetici più
alti e allora quello che ne risulta è uno spettro a “.righe di
emissione.”.
Tale spettro
è costituito dai fotoni che vengono emessi quando ciascun elettrone
ricade al livello più basso … gli elettroni degli atomi … possono
avere soltanto alcune energie molto specifiche, proprio
come specifiche, distinte e discontinue sono le altezze dei pioli di una
scala ... le righe d’emissione sono semplicemente … il prodotto di
transizioni verso l’alto. » (1)
(1)
Mike Inglis, “L’astrofisica è facile –
Un’introduzione per l’amante del cielo” – Springer
Verlag Italia, 2009
|
|
z “Spettri” e
“Righe di assorbimento”
z
|
|
|
|
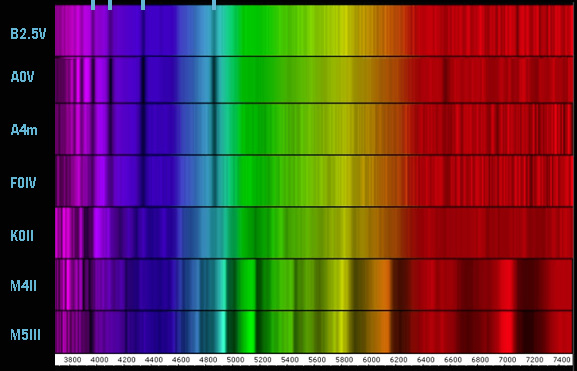
B2 è una stella
ad oltre 10.000 K, temperatura oltre la quale l’idrogeno comincia a risultare ionizzato, pertanto l’atomo perde i suoi elettroni, per cui
le righe statisticamente si formano
sempre meno al crescere della
agitazione termica … A ed F sono stelle
a temperatura intermedia per le quali le righe di Balmer dell’idrogeno (.le quattro indicate in azzurro.) sono
intense …
K ed M sono stelle a bassa
temperatura, per cui l’agitazione
termica non è ancora sufficiente ad eccitare gli atomi di idrogeno … le righe di Balmer sono assenti …
|
|
Z
Il
nome delle “Stelle”
z
|
|
|
|
z
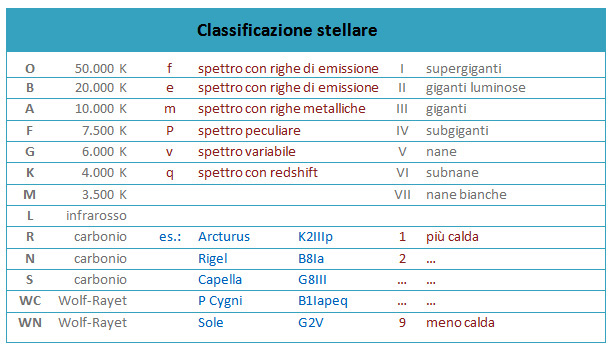
I numeri
romani possono essere seguiti da una lettera come “a” = più luminosa oppure “b” = meno luminosa
|
|
|