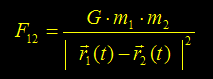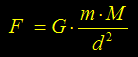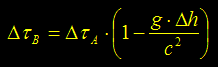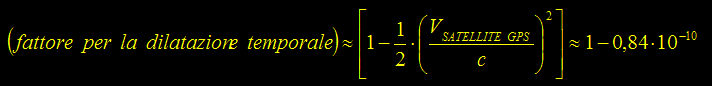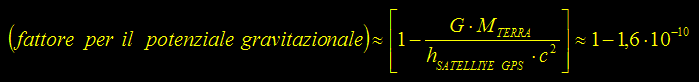|
Il pensiero di Newton resiste in mezzo a contraddizioni palesi - Premessa a Einstein |
||||||||||||||||||
|
z Per inerzia un corpo non soggetto a forze si muove di moto rettilineo uniforme. La gravitazione universale è valida tra riferimenti tra loro in moto relativo uniforme solo se consideriamo un tempo assoluto. Nel caso di riferimenti accelerati, entrano in gioco “forze fittizie” necessarie per far tornare i conti. Cassini riscontra ritardi e anticipi nel transito del satellite “Io” attraverso l’ombra di Giove, e attribuisce una possibile causa alla limitata velocità della luce. Ha dubbi e si lascia sfuggire l’occasione della scoperta, che viene portata a compimento dal suo allievo Römer. Römer (1678) dimostra, in modo definitivo, che la velocità della luce è finita e dal suo schema di misura se ne ricava anche una buona stima del valore numerico. Maxwell (1873) definisce le equazioni che uniscono loro campo magnetico e campo elettrico. Da esse emerge che la velocità di propagazione dell’onda deve essere sempre la stessa ed è relazionata in modo semplice a costanti facilmente misurabili della realtà fisica.
z |
||||||||||||||||||
|
z |
||||||||||||||||||
|
z |
||||||||||||||||||
|
z La sua velocità della luce è invariante rispetto al sistema di riferimento, perché dipende solo da grandezze fisiche assolute. Il suo pensiero è “troppo giusto” per poter minimamente pensare ad errori nella sua teoria. Tuttavia a lungo rimane questo problema d’incompatibilità con gli schemi del passato. Ogni spazio ha una sua “metrica”, cioè un metodo per definire la distanza elementare tra due punti vicini a piacere. Questa è la metrica euclidea di Galilei:
z |
||||||||||||||||||
|
La prima sintesi Einsteniana – lo “spazio-tempo” della Relatività Speciale |
||||||||||||||||||
|
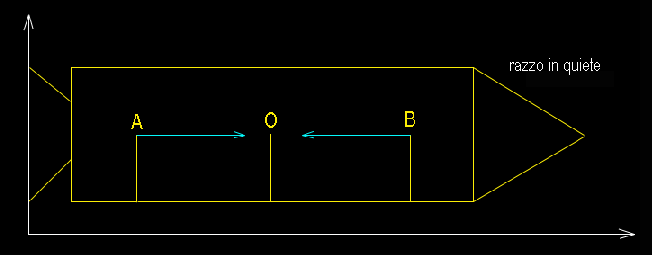
z È già evidente da Maxwell che la velocità della luce potrebbe essere un invariante. Si tratta di costruire una nuova visione della realtà che spieghi Maxwell e ammetta come caso limite Newton. Einstein procede per mezzo di “esperimenti mentali”. Vediamone uno, quello del razzo in quiete e in moto rettilineo uniforme: Supponiamo un razzo che contenga due sorgenti A e B e un osservatore O esattamente equidistante da esse. Sappiamo che O riceve un’informazione luminosa da A e da B nello stesso istante. Ipotizziamo che la velocità della luce sia
invariante rispetto al sistema di riferimento. z |
||||||||||||||||||
|
|
||||||||||||||||||
|
z La domanda che ci si pone è: l’accensione di A e quella di B sono contemporanee?
Sì, sono contemporanee. z |
||||||||||||||||||
|
|
||||||||||||||||||
|
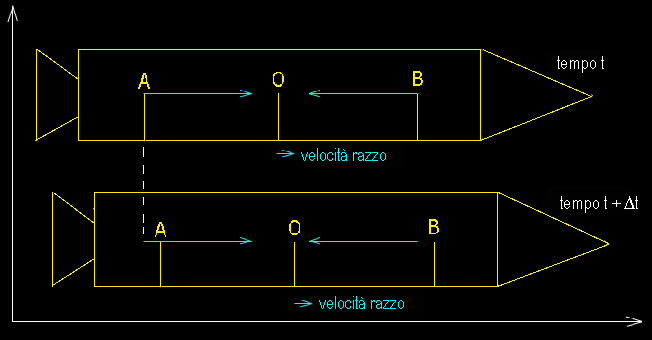
O deve vedere la stessa realtà, cioè riceve
contemporaneamente la luce da A e da B. Allora, muovendosi la
luce sempre con velocità“c”, diventa
evidente che nel nuovo sistema di riferimento i due eventi non sono più contemporanei. A deve partire prima e B dopo. z |
||||||||||||||||||
|
z |
||||||||||||||||||
|
z In una trasformazione inerziale generica di coordinate si passa da x, y, z, a nuove coordinate x’, y’, z’. Abbiamo ora osservato che anche la nozione di tempo cambia. Nulla di più semplice che considerare il tempo non più assoluto, ma come una coordinata che varia cambiando il riferimento. Ecco dunque il concetto di spazio-tempo quadridimensionale x, y, z, t. Si tratta ora di trovare una regola di
trasformazione che renda conto della realtà. Sarà la trasformazione di Lorentz con la
sua corrispondente “metrica”:
La velocità “c” della luce nel vuoto è un invariante e coincide con quella delle equazioni di Maxwell.
z |
||||||||||||||||||
|
Relatività Speciale - i “diagrammi spazio – tempo” |
||||||||||||||||||
|
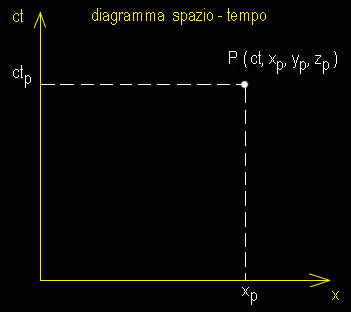
z
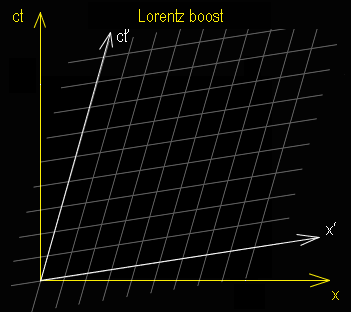
z La pendenza di una retta in questo diagramma vale: m = ct / x = c • ( t / x) = c / Vx se Vx = c allora m = 1, pertanto un fotone che viaggia a velocità “c” lascerà una traccia che è una retta a 45° gradi nel diagramma spazio-tempo. Una particella ferma sarà descritta da una retta verticale ( la x non cambia, il tempo sì ). « Nessuno si sognerebbe mai di confondere le distanze su una carta di Mercatore con le distanze fisiche sulla Terra. Una mappa di Mercatore è una proiezione della geometria del globo su un foglio di carta, che ha una geometria differente … Similmente, un diagramma spazio-tempo è la proiezione di una sezione bidimensionale di uno spazio-tempo con una geometria zzz su un foglio di carta con una geometria (1) James B. Hartle - “Gravity - An introduction to Einsten's General Relativity” - Addison
Wesley z |
||||||||||||||||||
|
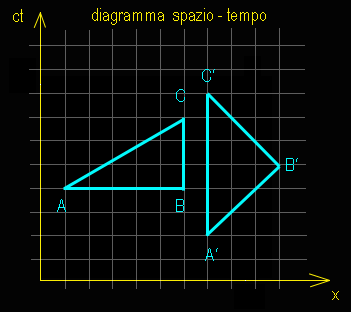
Relatività Speciale - i “diagrammi spazio – tempo” Vediamo con una figura queste asserzioni non esattamente intuitive, i conti sono fatti con le regole della trasformazione di Lorentz:
z Relatività Speciale - la “trasformazione di coordinate” Vediamo il caso di un sistema di riferimento con velocità uniforme rispetto a quello fondamentale. Si scopre che nel caso di moto uniforme lungo il solo asse x, la trasformazione porta ad un diagramma con la stessa origine, ma con assi ruotati
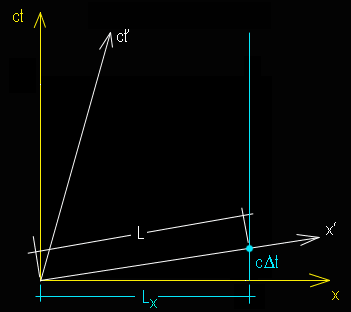
z Valutiamo la lunghezza Lx nel sistema
di riferimento fondamentale (regolo immobile) e la corrispondente lunghezza L nel riferimento in moto uniforme rispetto a “x” L. Ci accorgiamo subito che sono diverse e
che L può essere calcolata a partire da Lx e dalla
coordinata c • Dt applicando le
regole della trasformazione di Lorentz ( quindi non il teorema di Pitagora )
z « Con il successo della Relatività Speciale, divenne evidente che la gravitazione universale di Newton, che era stata applicata con successo alla meccanica del Sistema Solare per almeno 300 anni, non poteva ulteriormente essere considerata esatta. L’interazione gravitazionale Newtoniana è istantanea. La forza su una massa m1 dovuta ad una
seconda massa m2 è data in intensità dalla formula:
dove r1(t) e r2(t) sono le posizioni delle masse allo stesso istante di tempo. Ma nella Relatività Speciale la nozione di simultaneità è differente in differenti riferimenti inerziali. La legge di Newton potrebbe essere valida in un solo riferimento, e bisognerebbe distinguerlo da tutti gli altri. La legge di gravitazione Newtoniana è pertanto inconsistente con il principio di relatività ». (2) (2) James B. Hartle - “Gravity - An introduction to Einsten's General Relativity” - Addison
Wesley z Tutta la Relatività Generale (RG) si fonda su questa eguaglianza. La massa
Inerziale è quella che tende ad
opporsi alla azione di una forza:
La massa Gravitazionale è quella che compare nella legge di attrazione tra masse:
Gli scienziati hanno profuso
molte energie nella misurazione di questa eguaglianza con vari metodi. Quello
che possiamo dire è che essa è verificata nell’ambito della precisione degli
strumenti. È pertanto una realtà ben
assodata. z
La eguaglianza tra massa
Gravitazionale e massa Inerziale fa sperimentare in orbita una situazione di
“assenza di gravità”. Nella
navicella, effettivamente i corpi permangono in stato di quiete e, se spinti
leggermente, procedono di moto rettilineo uniforme. z In realtà il campo gravitazionale della Terra non è uniforme, ma ha simmetria radiale sferica e tende a diminuire allontanandosi dal centro del pianeta. Non è vero, pertanto, in senso stretto che in tutti i punti della navicella la gravità si annulli. Ma per spazi “piccoli” rispetto alla variazione del campo l’uguaglianza è sufficientemente valida. Pertanto la sua definizione, in “modo pratico” suona così: « Esperimenti in un laboratorio sufficientemente piccolo in caduta libera, su un periodo di tempo sufficientemente breve, danno risultati che sono indistinguibili da quelli degli stessi esperimenti in un sistema di riferimento inerziale in uno spazio vuoto » (3) (3) James B. Hartle - “Gravity - An introduction to Einsten's General Relativity” - Addison
Wesley Relatività Generale - Orologi in un campo gravitazionale Supponiamo di avere due osservatori con
orologi identici, immersi nel campo gravitazionale terrestre. L’orologio A ripete il
segnale con cadenza DtA e si trova ad
una altezza h. L’orologio B è posizionato a terra e avrà, in generale, una cadenza
DtB. Vale la
formula seguente:
Relatività Generale - GPS – Global Positioning System Le cadenze dei segnali provenienti dai satelliti del sistema GPS devono essere corrette, rispetto agli orologi a terra, perché i satelliti procedono a velocità elevata e perché si trovano ad un potenziale gravitazionale diverso rispetto a quello del comune utente. Il fattore di correzione per compensare la
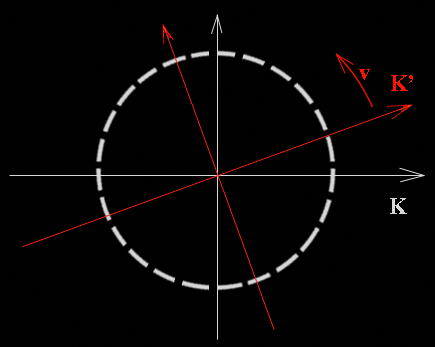
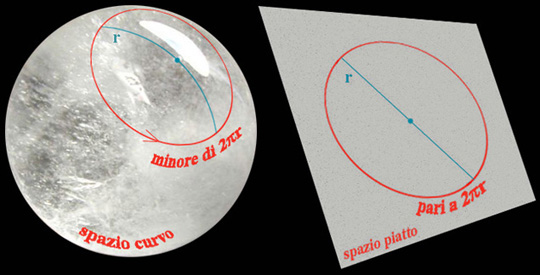
dilatazione dei tempi dovuta alla velocità dei satelliti vale: Relatività Generale - Lo Spazio-Tempo è curvo « Per chiarire meglio questo concetto consideriamo un sistema di riferimento inerziale K ed un sistema di riferimento K' non inerziale in rotazione uniforme rispetto a K. Consideriamo anche una circonferenza solidale con K. Rispetto a K il rapporto fra la circonferenza in quiete ed il suo diametro è pi-greco “π”. Rispetto a K' che ruota in senso antiorario la circonferenza viene vista ruotare in senso orario. Ogni piccolo segmento della circonferenza viene visto da K' muoversi con una certa velocità “v” [radiale].
In un certo istante ogni piccolo segmento di
cui è formata la circonferenza viene visto contrarsi rispetto a K' secondo la
legge della contrazione di Lorentz per
cui il rapporto fra circonferenza e
diametro è, rispetto a K', diverso da pi-greco “π” (il diametro non subisce la contrazione di Lorentz
perché non si muove rispetto a K' nel senso della sua lunghezza). Relatività Generale - Metrica La Metrica della Relatività Generale (RG) è una generalizzazione di quella della Relatività Ristretta ... z
z In È chiaro che la metrica, dipendendo dalla struttura dello
spazio-tempo in oggetto, dipende
da z |
||||||||||||||||||