 |
 |
z |
| Philosophiae
Naturalis PRINCIPIA Mathematica - 1687 |
| La grande impresa di Newton
è stata quella di far confluire le conquiste intellettuali di Galileo
e Keplero
in una fisica moderna ben strutturata.
L’opera di Newton
parte con una serie di definizioni di grandezze fisiche e con l’enunciazione
delle tre leggi del moto. Le fonti necessarie per comprendere l’opera sono |
|
z |
|
“Gli elementi”
di Euclide
“Le coniche”
di Apollonio
“Discorsi e dimostrazioni
matematiche, intorno a due nuove scienze attenenti alla meccanica et i
movimenti locali”
di Galilei, Del
moto equabile, proposizioni 1-2-4; Del
moto naturalmente accelerato, proposizioni
1-2; Del moto dei proietti,
proposizione 1 |
|
z |
| Keplero
compare in modo indiretto: utilizzando le definizioni e le tre leggi della
dinamica, le sue leggi sono dimostrate, non impiegate quindi come ipotesi
di partenza.
Newton ha
una visione cosmologica della meccanica; Galileo
ne ha una visione semplicemente terrestre. Un proiettile che cade segue
in realtà un’orbita ellittica, e se avesse sufficiente velocità
si porrebbe in orbita attorno alla Terra. Trascriviamo le parole autografe
di Newton,
prese dai “Principia”
- Libro I - Scholium:
«… Se
il centro d’attrazione si sposta all’infinito, l’ellisse si trasforma in
una parabola, il corpo si muoverà su una parabola
…» |
|
|
| 1a legge |
Principio d’inerzia ("vis
insita")
- Ogni corpo continua nel suo stato di quiete o di moto uniforme in linea
retta, a meno che non sia soggetto a forze che alterano il suo stato -
[ipotesi ragionevole
che Newton dice di derivare da Galilei]. |
|
I contemporanei del "lucasian
professor"
affermano che il concetto compiuto d’inerzia
appartiene a Cartesio.
Il nostro non lo accetta perché la sua meccanica meccanicistica
e metafisica non può essere condivisa da un fautore del metodo scientifico. |
|
È vero altresì che lo spazio di
Cartesio,
con i famosi assi da cui si dipartono semirette che vanno all’infinito,
può consentire il moto rettilineo uniforme (difficile
però è renderlo compatibile con l’ipotesi dei vortici onnipresenti). |
|
Galilei afferma
che un corpo permane nel suo stato di moto imperturbato su una superficie
sferica attorno alla Terra:
« ... e però,
rimossi tutti gl'impedimenti esterni, un grave nella superficie sferica
e concentrica alla Terra sarà indifferente alla quiete ed a i movimenti
verso qualunque parte dell'orizonte, ed in quello stato si conserverà
nel qual una volta sarà stato posto; cioè se sarà
messo in stato di quiete, quello conserverà, e se sarà posto
in movimento, verbigrazia verso occidente, nell'istesso si manterrà:
e così una nave, per essempio, avendo una sol volta ricevuto qualche
impeto per il mar tranquillo, si moverebbe continuamente intorno al nostro
globo senza cessar mai, e postavi con quiete, perpetuamente quieterebbe,
se nel primo caso si potessero rimuovere tutti gl'impedimenti estrinseci,
e nel secondo qualche causa motrice esterna non gli sopraggiugnesse ...
» (*) |
|
Inoltre lo spazio di Galilei
è limitato e non può, filosoficamente parlando, accettare
traiettorie rettilinee infinite:
« ... De i
luoghi dove collocar la stella nuova [la
nova di Tycho del 1572], alcuni son manifestamente
impossibili, ed altri possibili. Impossibile assolutamente è che
ella fusse per infinito intervallo superiore alle stelle fisse, perché
un tal sito non è al mondo, e quando fusse, la stella posta là
a noi sarebbe stata invisibile ... »
(**) |
|
La verità è che ciascuno dei due
ha dato un grosso contributo al concetto d’inerzia, Galileo
in modo quasi esaustivo, salvo contraddizioni finali, ma solo Newton
lo esprime in modo totalmente corretto. |
| 2a legge |
Accelerazione proporzionale alla Forza,
nella direzione della forza stessa - una novità assoluta - [ipotesi
ragionevole] |
| 3a legge |
Principio d’azione e reazione,
- Ad una azione corrisponde sempre una reazione uguale e contraria; oppure:
le mutue azioni di due corpi sono sempre uguali e dirette in versi contrari
- una novità assoluta - [ipotesi
ragionevole] |
|
|
| Queste tre leggi
(ipotesi ragionevoli
di lavoro trovate mediante osservazione dei fenomeni, induzione e deduzione)
assieme alle definizioni, sono tutto ciò che è necessario
a Newton
per dimostrare la validità della gravitazione
universale. Alcuni dati osservativi (Fenomeni)
danno conferma della bontà del suo pensiero.
Newton è
stato anche fondatore, in modo indipendente da Leibnitz,
della analisi infinitesimale. Avrebbe potuto in poche pagine rappresentare
in modo compiuto la sua gravitazione universale, invece decide di raccontarla
con “metodo
geometrico”,
probabilmente perché avrebbe così raggiunto una diffusione
più ampia, visto la cultura matematica dei suoi contemporanei.
Come fa Newton
a mescolare Forze e Geometria per arrivare
al risultato?
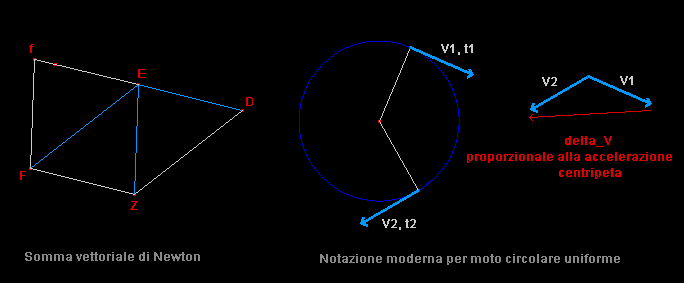
Egli ha molto chiaro in mente che velocità
e forza sono vettori, cioè hanno una intensità, una direzione
e un verso, pertanto rappresentabili con segmenti orientati [Newton
userà semplici segmenti sottintendendo l'orientamento].
Inoltre intuisce come i vettori si compongono, e pertanto ricava da una
ipotetica variazione di velocità [necessita
dunque considerare due punti distinti P
e Q]
su una traiettoria curva, la direzione della
accelerazione, e quindi, per la seconda legge, anche della forza. |
|
 |
| Utilizzando Euclide
e Apollonio
egli riesce a ricavare una relazione tra la forza e il raggio vettore che
va dal fuoco ai punti. Effettua
un passaggio al limite, portando a coincidere
tra loro i due punti, e ciò che rimane è la proporzionalità
inversa della forza col quadrato del raggio vettore.
Ma vediamo, con le parole autografe di Newton,
come si configura il problema: |
|
|
| ecco dunque,
con parole moderne [e.g.
massa = quantità di sostanza]
la formulazione della conclusione: |
| Tesi o
4a legge |
Gravitazione universale:
la forza è direttamente proporzionale al prodotto delle masse e,
inversamente, al quadrato della distanza. La legge contiene un fattore
invariabile "costante
universale",
misurata per la prima volta da Cavendish con la bilancia di torsione. |
z
(*) |
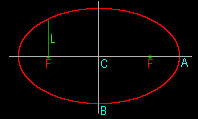
L è
il “latus
rectum” della
ellisse:
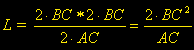 |
 |
|
|
dove BC
è il semiasse minore e AC
è il semiasse maggiore. Data l’ellisse, dunque, L
è una costante. |
(*) Galilei,
Galileo, «Seconda lettera del sig. Galileo
Galilei al sig. Marco Velseri delle macchie solari».
tratto da Liber Liber.
(**) Galilei,
Galileo, «Dialogo sopra i due massimi
sistemi del mondo». tratto da Liber
Liber.
Fanno parte del "Progetto
Manuzio", che è una iniziativa dell'associazione
culturale Liber Liber. Aperto a chiunque voglia collaborare, si pone come
scopo la pubblicazione e la diffusione gratuita di opere letterarie in
formato elettronico. Ulteriori informazioni sono disponibili sul sito Internet:
http://www.liberliber.it/ |
 |