| Breve storia dell’astronomia
da Ipparco a Einstein
Ipparco da Nicea
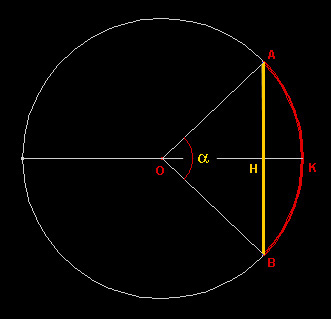
Ha sviluppato la matematica del suo tempo e costruito le prime tabelle trigonometriche, ha risolto diversi problemi di geometria sferica. Egli ha tabulato i valori per la funzione corda, che dà la lunghezza della corda per ogni angolo. Lo ha fatto per un cerchio con una circonferenza di 21.600 e un raggio (arrotondato) di 3.438 unità. Egli aveva tabulato le corde per incremento di angolo pari a 7,5 °. In termini moderni, la corda di un angolo uguale a due volte il seno dell'angolo metà, vale a dire: z
z
C
Studiando le osservazioni degli antichi si è accorto che non coincidevano più esattamente con le sue, e da questo fatto ha dedotto due tipi di conseguenze: (1) l'esistenza di un moto che produce la precessione degli equinozi, (2) il moto proprio delle stelle. Sulla base di queste scoperte ha quindi proceduto alla compilazione del primo catalogo stellare completo del mondo occidentale. Quest'ultimo rappresenta la posizione degli astri mediante Latitudine e Longitudine, che sono di fatto una sua scelta originale. A lui è attribuita l'invenzione dell’astrolabio e della sfera armillare la cui prima comparsa fu durante il suo secolo. Egli, probabilmente, lo utilizzò come ausilio per la creazione del catalogo stellare. Ipparco fu il primo a dimostrare che la proiezione stereografica è conforme, e che trasforma cerchi sulla sfera che non passano attraverso il centro di proiezione in cerchi sul piano. Questa è stata la base per l'astrolabio. Ha stimato altresì una distanza Terra-Luna sufficientemente corretta. Con le sue teorie solari e lunari e la sua trigonometria, egli potrebbe essere stato il primo a sviluppare un metodo affidabile per prevedere le eclissi solari. G. Toomer, storico dell'astronomia, ha suggerito che la conoscenza delle eclissi da parte di Tolomeo ed altre osservazioni babilonesi nell’Almagesto provenisse da una lista fatta da Ipparco. Queste, di tre secoli prima, sono le fonti di
Claudio Tolomeo
che completò il lavoro di Ipparco;
la sua sintesi è fortemente dipendente dalle scoperte del nostro
in molti settori.
Claudio Tolomeo di Alessandria visse nel II secolo d.C., probabilmente tra il 100 e il 170 circa. Quel che sappiamo sulla sua vita lo desumiamo dai riferimenti cronologici che ci fornisce. La prima notizia del suo lavoro risale al 127 d.C. l’undicesimo anno dello spagnolo Adriano, uno degli imperatori più colti che salirono sul trono di Roma. La datazione del suo catalogo stellare è del 137 d.C., il primo anno del regno di Antonino, e l’ultima datazione a noi pervenuta risale al 150. Visse quindi in un periodo culturale particolarmente felice. La sua città natale, Alessandria, era stata un centro di vita e di potere, oltre che cuore della cultura ellenistica. Qui il sapere si specializzò e cercò di definirsi in modo autonomo, affrancandosi dalla religione e conseguentemente da qualsiasi forma di dogmatismo. Rimane però un profondo divario dalla scienza moderna nell’atteggiamento, che sviluppò essenzialmente l’aspetto teoretico, senza tentare l’applicazione pratica di quanto studiato. Tolomeo è l’erede della grandezza di questa città e di ciò che fu. Scrisse molto, e molto ci è pervenuto. Il suo scritto più conosciuto ed importante rimane la Sintassi matematica, Mathematiké Syntaxis, che costituisce una summa dell’astronomia antica. « I
posteri la chiamarono Somma Sintassi,
usando il superlativo meghiste,
« grandissimo
» (da megas,
« grande
»). Gli Arabi lo tradussero con Al
Majisti, che fu a sua volta ritradotto
in Almagesto.
Di qui il suo strano nome, che si potrebbe parafrasare con «
Somma Summa »,
o « Maestoso
Trattato ».
Quest'opera conclude il grande e glorioso periodo della matematica greca
ed ellenistica ... in seguito, per circa un millennio, la matematica emigrerà
altrove: in particolare, nei paesi arabi
» ( "C'è spazio per
tutti" - Piergiorgio Odifreddi - Mondadori ).
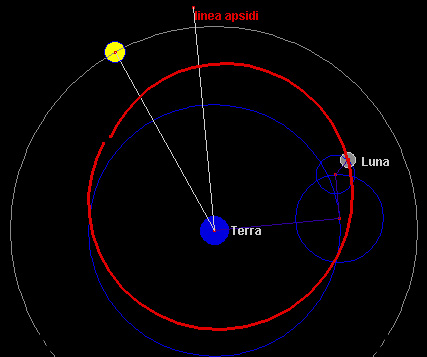
Claudio Tolomeo Tolomeo considera per ciascun pianeta un deferente il cui centro è spostato in maniera opportuna rispetto al centro della Terra. Questo disassamento rende ragione del fatto che quando il Pianeta / la Luna è più lontano si muove apparentemente più lentamente. È la sensazione che abbiamo osservando barche analoghe in mare: quella lontana sembra quasi ferma, mentre quella vicina in breve tempo esce dal nostro campo visivo. Il moto circolare uniforme sul deferente rappresenta il "moto siderale attorno alla Terra" della "stella errante" ( pianeta ). L’eccentricità del deferente copre l’esigenza osservativa della "prima disuguaglianza". Questo scostamento rende ragione del movimento rallentato del pianeta quando è più lontano. Il deferente eccentrico, tuttavia, non rende ragione completa del moto osservato. Le longitudini negli apsidi e nelle quadrature vanno bene, ma non quelle agli ottavi. Ecco dunque la necessità di un epiciclo di dimensione opportuna e con rotazione opportuna tale da correggere queste discrepanze. L’epiciclo copre l’esigenza osservativa della
"seconda disuguaglianza".
Essa è dovuta al fatto che la velocità del Pianeta / della
Luna è più lenta apparentemente quando sono più lontani,
ma lo è anche in valore assoluto. È un tentativo di approssimazione
per adattarsi al moto variabile sull’ellisse, non perfetto perché
sarebbero necessari infiniti epicicli, i più piccoli infinitesimi,
per perfezionare il moto. Siamo, quindi, in
presenza di un modello "imperfetto". Esso, tuttavia, fu soddisfacente per
un millennio e mezzo, fino a Copernico,
perché la precisione di misura era così bassa che scostamenti
a questo livello di dettaglio erano di fatto ininfluenti. Lo
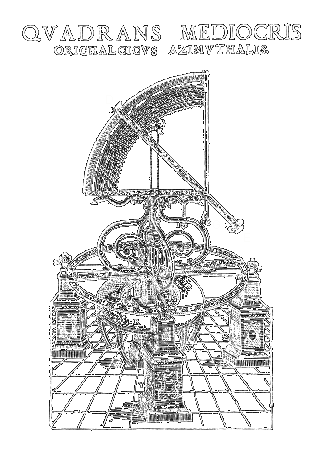
strumento principe di misura era la "ballestriglia"
o "bastone
di Giacobbe",
una croce graduata con braccio corto mobile. Essa era di dimensioni modeste
(poteva essere trasportata facilmente e usata da una sola persona), pertanto
la precisione angolare era di 0,5°
( pari al diametro della Luna
).
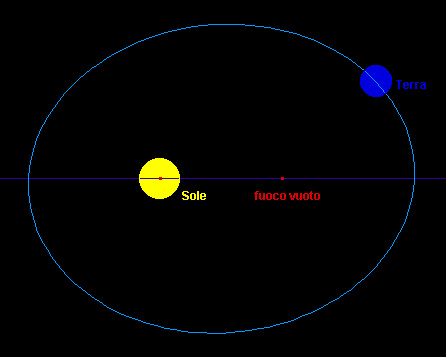
Niklas Koppernigk nacque a Torùn (ted. Thorn) sulla Vistola, dove il padre aveva raggiunto col proprio lavoro di mercante una discreta posizione sociale. Nel 1491 Koppernigk, che latinizzò il proprio nome in Copernicus, si recò presso l’università di Cracovia. Qui erano in competizione due correnti di pensiero: quella dei naturales (fisici cosmologici), e quella dei matematici (astronomi interessati al calcolo delle posizioni dei corpi celesti, e al controllo delle previsioni attraverso l’osservazione). I naturales erano fedeli al pensiero aristotelico e al sistema delle sfere omocentriche, i matematici avevano invece come testo base l’Almagesto tolemaico e il sistema calcolatorio degli eccentrici e degli epicicli. Nella diversità, le due teorie presentavano però alcuni punti in comune, come la centralità universale della Terra e l’idea che il moto celeste fosse circolare uniforme. Il sistema delle sfere omocentriche non riusciva a giustificare il fatto, che i pianeti appaiano ora vicini ora lontani (ciò vale in modo vistoso per Marte, che passa da 56 a più di 400 milioni di chilometri dalla Terra; un fattore 7 nelle dimensioni apparenti); il sistema degli eccentrici e degli epicicli era costretto, al fine di spiegare adeguatamente la realtà osservata, ad elaborare ipotesi precise che supplissero alle mancanze del sistema stesso, il quale in tal modo rischiava di essere invalidato. È chiaro dunque che nella sostanza già Tolomeo aveva superato il pensiero di Aristotele. La comunanza stava nel fatto che entrambi avevano la Terra al centro. Copernico riprende motivazioni e studi arabi, ponendo il Sole fermo nel suo cosmo e la Terra in moto (anch’essa pianeta come gli altri). In verità si tratta di una concezione "eliostatica" e non "eliocentrica" in quanto il Sole di Copernico è il "Sole medio". Esso è una astrazione che non ha corrispondenza osservativa. Si tratta di un Sole che fa il suo percorso annuale nello stesso tempo del "Sole astronomico", ma con moto uniforme. Il Sole medio è molto comodo per calcolare le effemeridi. Copernico non dice in modo chiaro quale sia il centro del suo cosmo. Agli studiosi appare evidente che esso coincida col centro dell’orbita della Terra, un punto vuoto nello spazio. Il "Sole astronomico" infatti è eccentrico, perché d’estate qui da noi è più lontano e d’inverno più vicino. Ciò era noto. Otto Neugebauer, uno dei massimi studiosi di Tolomeo e di Copernico, annota come il nostro non abbia prodotto significativo valore aggiunto nel moto dei pianeti, che in modo semplificato sono andati soggetti ad un mutamento di sistema di riferimento (dal centro della Terra, al centro della sua orbita). Copernico perfeziona invece il moto della Luna, rendendo la sua orbita molto più probabile di quella di Tolomeo. Dal punto di vista quantitativo (effemeridi),
le tabelle di Copernico
non superano di fatto quelle del Tolomeo.
Il metodo di calcolo è naturalmente molto differente. Ciò
è semplicemente legato al fatto che, ancora alla sua epoca, le misurazioni
erano fatte con la "ballestriglia". Era pertanto non sperabile ottenere
miglioramenti nelle predizioni.
Tyge Brahe, latinizzato Tycho, nacque in Danimarca nel 1546 e morì nel 1601. Protetto da Federico II di Danimarca, ebbe in dono dal sovrano l’isola di Hven nello stretto di Copenaghen, oltre a uno stipendio, che gli concesse una grande autonomia di studio e di ricerca. Ebbe una disponibilità economica che gli permise di costruirsi un castello, un osservatorio, laboratori e persino una stamperia privata. Per vent’anni, dal 1576 al 1597, si dedicò all’osservazione degli astri con l’aiuto di numerosi assistenti. Da Copernico non vi era stato progresso in ambito astronomico, e qualcuno cominciò a teorizzare la necessità di un approccio diverso. Brahe aveva capito la necessità di nuovi dati osservativi e ritenne fondamentale impegnarsi per costruire strumenti, che migliorassero la percezione e potenziassero le facoltà umane. Un atteggiamento estremamente aperto per l’epoca, che lo spinse a creare macchinari di eccezionale grandezza e precisione, con i quali poté lasciare informazioni fondamentali per il lavoro successivo. La decisione di procedere in tale senso viene dalla osservazione che la congiunzione di Giove e Saturno avvenuta il 26 agosto 1563 era errata, secondo le effemeridi note, di un mese. Tycho valuta che tale discrepanza fosse dovuta ad osservazioni imprecise. Egli è la persona giusta al momento giusto, perché nel frattempo era venuta matura la tecnologia del bronzo, che gli permetterà di realizzare grandi strumenti di altissima precisione. Brahe procede diligentemente e con caparbietà alla misura di quasi un migliaio di stelle e di straordinari dettagli dei pianeti, specialmente di Marte. Egli non accoglierà il modello di Copernico, ma ne elaborerà uno equivalente, con al centro la Terra. Pertanto il Sole rivoluziona attorno alla Terra, e i Pianeti rivoluzionano attorno al Sole. Facendo così l’orbita del Sole interseca quella dei pianeti, in particolare Marte risulta talora più vicino alla Terra (56 milioni di chilometri) che non il Sole (150 milioni di chilometri). Oggi noi sappiamo che è davvero così, ma la sensibilità di allora lo percepiva come un corpo estraneo. Tycho applica le sue misure al suo modello cosmologico, ma non trova corrispondenza. Il fatto è che egli ha osservazioni trenta volte più precise di quelle precedenti (1 primo, invece di trenta), che non trovano corrispondenza in modelli che sono stati dimensionati sulla base di dati meno affidabili. Si tratta di una matassa maledettamente ingarbugliata
di cui egli non riesce a trovare il bandolo.
Vorrebbe agire in proprio, perché è gelosissimo delle sue
misure, di cui comprende il grande valore. Ha
anche il desiderio di passare alla storia, e ciò lo convince a prendere
come assistente un astronomo dalle grandissime capacità matematiche.
Tycho
muore prematuramente, con molte traversie i sui dati finiranno nelle mani
dell’assistente che nel frattempo ha ricoperto il suo ruolo.
Johannes Kepler, latinizzato Keplero, nacque il 27 dicembre 1571 a Weil, vicino a Stoccarda. Da Caterina Guldenmann, figlia di un oste, e da Enrico, funzionario di religione luterana, al servizio del Duca di Brunswick, che partì con la moglie come mercenario contro i Belgi nelle schiere del Duca di Alba, lasciando il figlio in tenera età ai nonni. Di salute delicata, Johannes sopravvisse al vaiolo, che gli lasciò però le mani danneggiate e una vista debole. Da Brahe ebbe l’invito di rivedere il sistema ticonico alla luce delle sue scoperte, da Galilei un’interessante risposta, nella quale si esprimeva il rammarico per il clima di derisione e stoltezza verso le ipotesi copernicane, e verso la ricerca della verità. Pitagora, Platone e il pensiero cabbalistico forniscono gli strumenti, e condividono con Keplero un mondo ordinato, strutturato geometricamente; un universo mitico ed ideale, a cui Keplero attribuisce giudizi di valore. Solo le misurazioni perfette di Brahe, lo costringeranno a desistere dalla teoria della perfezione circolare del moto astrale, e a piegarsi al moto ellittico, mentre affrontava il problema del moto irregolare di Marte, ancora irrisolto, al quale lavorò indefessamente per dieci lunghi anni, e di cui ci ha lasciato un’entusiasmante descrizione. Nulla accade per caso, Keplero risulterà vincente per merito anche di una sua rustica convinzione cosmologica, e cioè che il Sole è un gran magnete rotante che trascina attorno a sé i pianeti. Questa azione si indebolisce con la distanza, pertanto, i pianeti più lontani sono anche i più lenti. È chiaro, da quanto esposto, che Keplero
fa riferimento al "Sole astronomico",
nel suo gergo il "Sole
osservato"
e non il "Sole medio". Questo sarà un "incipit" chiave che lo potrà
condurre alla soluzione definitiva.
Anche lui proverà ad inserire i dati di Tycho nel sistema copernicano, ma senza successo. Si chiede il perché di tale non corrispondenza, e si dà una prima spiegazione: Tycho ha misurato dalla Terra, e lui (Keplero) tenta di trasporre quei dati in un sistema eliostatico; ma l’orbita della Terra (o quella del Sole, il che è del tutto equivalente) era nota con la precisione di 30 primi e non un primo come richiedevano i nuovi dati. Mediante triangolazioni Marte-Terra-Sole, con Marte nella stessa posizione siderale, egli costruisce tre punti dell’orbita della Terra, supposta per il momento circolare. Ricava così il valore di eccentricità di quest’orbita che risulta essere la metà di quanto supposto dai predecessori. Modifica il modello copernicano con questo nuovo valore e ritenta l’avventura di inserire i dati di Tycho: il grosso dell’errore è risolto, rimane una imprecisione, rispetto all’osservato, di 8 primi. Molti ne sarebbero andati a casa soddisfatti, ma non Keplero, che sapeva che i dati nuovi avevano la precisione di 1 primo. Egli accorda fiducia totale a queste misure. Si accorge che la forma dell’orbita di Copernico non potrà mai adattarsi alle misure. Bisogna ipotizzare una curva di tipo nuovo. Non pensa all’ellisse, perché se quella fosse stata la soluzione, secondo lui gli antichi gia la avrebbero scoperta. Dopo molti tentativi, si accorge però che l'ellisse avrebbe potuto essere la soluzione. Prova e tutto, miracolosamente, va a posto. Il "Sole astronomico" sta in un fuoco, quindi fuori da una qualunque simmetria. Il mito del moto circolare uniforme cade, per lasciare posto al moto ellittico non uniforme. Egli riesce anche a determinare la legge del moto. Le misure erano precise quanto basta da consentire ciò, e imprecise quanto basta da non mettere in crisi questa ipotesi. Galilei scopre, tramite le macchie solari, la rotazione del Sole, e questo dà un grande conforto osservativo al nostro. I satelliti di Giove seguono ellissi kepleriane. Il modello ha dunque una validità generale, si presta per i pianeti e per i satelliti. Nella visione di Keplero
solo il Sole
agisce, i Pianeti
sono passivi e tra di loro non si disturbano.
I pianeti, inoltre, sono assunti come puntiformi. Una
zona buia rimane ancora in mezzo a tanto successo: la
Luna presenta
delle irregolarità di moto
che non possono essere spiegate dalla legge delle ellissi.
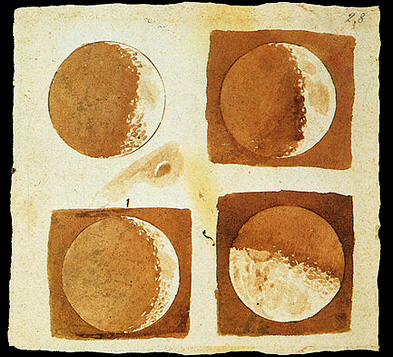
Galileo Galilei nacque a Pisa il 15 febbraio 1564. Il padre Vincenzo era un musicista ed un commerciante. La madre era Giulia Ammanati. Sappiamo, da una registrazione del 1581, che studiò presso lo Studio pisano come artista. Probabilmente doveva divenire medico, ma ben presto si dedicò completamente alla matematica, con il maestro Ostilio Ricci, discepolo di Niccolò Tartaglia Utilizzando il cannocchiale, giungerà alle scoperte registrate nel Sidereus Nuncius (1610), che lo renderanno immediatamente famoso, tanto da ottenere dal Granduca Cosimo II de’ Medici, il ruolo di "matematico straordinario di Pisa" - senza nessun obbligo, né di residenza né di lezione -, nonché di "filosofo del Serenissimo Duca". In quest’opera egli espone le scoperte, compiute con il cannocchiale. In primo luogo un numero elevato di nuove stelle, che cambierà l’immagine precedente del nostro universo, che in tal modo diveniva più grande. Il cannocchiale ha un pregio enorme: avendo 20 ingrandimenti, in concreto migliora di un fattore uguale la precisione di misura. Non corrispondenze alle ellissi di Keplero sorgono anche nell’ambito dei Pianeti e non solo della Luna. Ci deve essere qualcosa di nuovo, che solo qualche persona davvero straordinaria potrà svelare. Si intuisce che forse i pianeti si perturbano
l’un l’altro. Si intuisce che forse approssimare ad un punto non sempre
va bene. Come affrontare il problema?
Isaac Newton nacque nel 1643. Studiò nel Trinity College di Cambridge. Ebbe come insegnante di matematica Isaac Barrow (1630-1677), autore delle interessanti Lectiones mathematicae, che resosi conto delle doti dell’allievo, lo incoraggiò a proseguire sulla strada dello studio, che lo aveva già portato alla conoscenza del calcolo delle flussioni, cioè il calcolo infinitesimale, che utilizzava già per risolvere alcuni problemi di geometria analitica. È del 1684 il celebre incontro tra Halley, Wren e Hooke, che coinvolse Newton, e a cui seguì la pubblicazione dei Philosophiae Naturalis Principia Matematica. In questa importantissima opera spiegava la teoria di Keplero sulla tesi copernicana, per mezzo dell’ipotesi di una gravitazione verso il centro del Sole decrescente secondo l’inverso dei quadrati delle distanze e proporzionale alla quantità di materia solida dei pianeti. Questo libro è l’armonizzazione di tutte le teorie precedenti, unendo Copernico, Cartesio, Keplero e Galilei in un unicum, in cui finalmente viene spiegato il grande libro della natura. Partendo da una visione corpuscolare della realtà, si usa la matematica per capirne la struttura. Newton in sostanza dice: "tutto attrae tutto" e trova anche la legge che bisogna applicare per fare di calcolo. La forza tra due corpi è proporzionale al prodotto delle due "quantità di materia" (masse) e inversamente proporzionale al quadrato della distanza. Partendo da qui egli ricostruisce come caso particolare le tre leggi di Keplero. Il valore aggiunto è enorme ed è dovuto agli studi matematici giovanili. Newton trova lo sviluppo in serie della potenza di un binomio dove uno dei due addendi sia abbastanza piccolo. Questo permette, troncando al serie ad un numero di termini ragionevole, di fare di calcolo e di capire quali sono le entità che controllano le perturbazioni maggiori. Nelle equazioni differenziali che la gravitazione
universale propone (e che l’analisi infinitesimale
di Newton è in grado di affrontare)
spesso compaiono a denominatore binomi in cui un termine è moltiplicato
dalla eccentricità, che assume per il sistema solare valori molto
piccoli. Si può allora sviluppare
in serie numerica e troncare alla precisione voluta.
Questa possibilità permette di capire a quali cause sono dovute le principale interferenze planetarie. Permette altresì di studiare l’influenza di corpi oblati (panciuti all’equatore a causa della rotazione) e con l’asse di rotazione inclinato. Le ellissi di Keplero non sono più chiuse, perché, a causa delle perturbazioni, ruotano lentamente e nel tempo la linea degli apsidi cambia orientamento. Il sistema Terra-Luna-Sole, studiato con modello del "problema dei tre corpi ristretto", permette di rendere conto delle non rispondenze alla ellisse kepleriana. Newton non riuscirà a risolvere "in toto" il problema solo perché utilizzerà un numero troppo ridotto di termini della serie polinomiale. La legge però è giusta. Dimostra così che l’orbita della Luna ruota in 18,6 anni (cosa nota fin dall’antichità, ma mai spiegata), si dimostra che l’evezione è funzione della elongazione della Luna rispetto al Sole e del suo moto anomalistico (moto già noto a Ipparco). Un sistema a tre corpi mostra di essere intrinsecamente instabile (almeno sul lungo termine), salvo soluzioni particolari che troverà Laplace. La gravitazione di Newton, pertanto, introduce il caos nel sistema solare. Tutti sappiamo come Giove, perturbando le loro orbite, spesso renda instabili asteroidi della fascia tra lui e Marte, proiettandoli verso il sistema solare interno. Le comete spesso hanno orbite caotiche, anche se sono regolari a tratti. Molti moti (e.g. precessione) prima studiati solo con opportuni moti cinematici di sfere, ora trovano una esauriente spiegazione fisica. Oggi la gravitazione universale è facilmente
integrabile numericamente, per cui molti sono coloro che riescono a produrre
effemeridi affidabili con mezzi modesti. Una vera rivoluzione!
Albert nasce a Ulma, in Germania, il 14 marzo 1879, da padre, Hermann, e madre, Pauline Kock, ebrei non praticanti. Nel 1880 l’impresa familiare verte in difficoltà, e l'intera famiglia si sposta a Monaco, dove il padre apre, col fratello Jacob, ingegnere, una piccola fabbrica. La fisica newtoniana si basa sul concetto elementare astratto di punto materiale, o particella, quindi la materia è considerata discontinua a priori. È noto come Newton sia stato un grande fautore della teoria corpuscolare della luce. Come si spiegano i fenomeni meccanici nell’ambito di questo contesto? È ipotizzata la "azione a distanza" tra punti materiali, con effetto immediato. Sembrava ormai che il metodo di Newton potesse dare risposta a tutta la meccanica. Un problema sorge, però, quando, nella seconda metà del XIX secolo, diventano note le leggi della elettrodinamica di Maxwell. Esse, infatti, non possono essere incorporate in maniera soddisfacente nel sistema newtoniano. Maxwell determina nel dettaglio queste leggi che trovano la loro espressione naturale nelle equazioni differenziali per i campi elettrico e magnetico. In particolare riscontra che l’onda elettromagnetica si deve propagare con una velocità costante e finita, il cui valore è fornito dalla misura di grandezze caratteristiche dell’ambiente circostante. Per far tornare la velocità della luce finita e costante in tutti i riferimenti inerziali ci vorrà la relatività ristretta (RR). Per far tornare l’eccedenza di precessione del perielio di Mercurio ci vorrà la relatività generale (RG), che con la deformazione dello spazio circostante spiega il fenomeno. Anche Einstein
ha però i suoi limiti: non riesce a spiegare quella singolarità
che si chiama "buco
nero". Per
tentare di dominare ciò ci vorrà la meccanica quantistica.
Ma le due sono al momento due mondi separati e la sintesi appare ancora
lontana.
z |
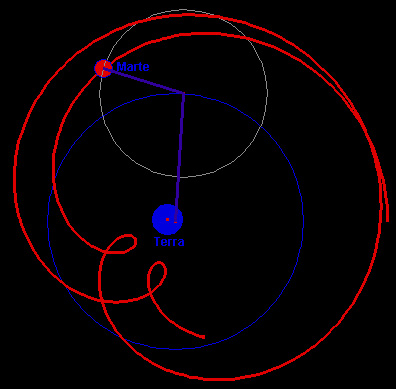 image
credit: Pighin
image
credit: Pighin