 a Giove tabellare
Il "Solarscope"
e l'osservazione del Sole
a Giove tabellare
Il "Solarscope"
e l'osservazione del Sole
Questo strumento è dotato di un sistema
ottico di lenti convergenti, che porta l’immagine su uno specchio metallico
sferico che funziona da ingranditore. L’immagine
del Sole viene
proiettata su uno schermo bianco dove è disegnato un cerchio graduato
di riferimento di dimensioni pari al massimo diametro del Sole proiettato.
image credit Sandro
Arpe  image credit Sandro Arpe
image credit Sandro Arpe |
L’osservazione è pertanto sicura
e permette di vedere un Sole
di dimensioni pari a circa 10 cm. È facile, pertanto, poter osservare
con comodità la presenza di macchie
solari. |
Il "Sole
osservato" in estate e in inverno
|
Osservando
il Sole,
tutti i giorni lungo l’arco di un anno, si scopre che le
sue dimensioni sul foglio variano in funzione della stagione.
image credit Giampiero Barbieri
In inverno alla data del 3 gennaio,
la sua dimensione è massima.
In estate alla data del 4 luglio,
la sua dimensione è minima.
z
z
Il "Sole
osservato" in estate nel nostro emisfero ...
In estate il Sole
si vede più piccolo
semplicemente perché è più
lontano ... e sarà anche più
lento per due ragioni ...
| 1) |
Una barca a vela che ci transita
davanti a 100 metri appare relativamente veloce, ma una simile all'orizzonte
appare muoversi molto più lentamente ... analogamente in
estate il Sole appare più lento perché più lontano
... |
| 2) |
Keplero con
la sua 2^ legge
ci dice che anche la velocità di
rivoluzione è più lenta
... lo vediamo con la formula seguente dove di vede che "V"
( velocità ) è inveramente proporzionale all'inverso della
radice del raggio vettore Terra-Sole ( "r"
nella formula ) |
|
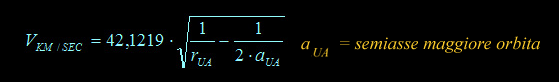 |
Se il moto di rivoluzione del Sole
( gradi / giorno ) è variabile, anche
la durata del "giorno solare vero"
( combinazione di rotazione siderale e moto di rivoluzione ) sarà
variabile nell'arco
dell'anno e quindi sempre un po' diversa
dal "giorno
solare medio" pari a 24
ore esatte ...
Se i "giorni
solari veri"
si scostano ( per esempio in meno ) in un dato periodo, ecco che cumulativamente
nel tempo si possono avere variazioni del
Sole osservato
anche di parecchi minuti ...
Se il Sole
è talora più vicino e talora più lontano, ciò
significa che la sua orbita è ellittica
( Kepler docet ...
) con la Terra
in un fuoco ...
z
Calcolo della "eccentricità"
del sistema Terra-Sole
z |
Prendiamo le due foto del Sole
proiettato a queste due date … le ridimensioniamo
in modo che la griglia di riferimento sia identica nei due casi
… ciò permette di poter misurare, esattamente con un righello, la
differenza di dimensione tra il Sole
invernale e quello estivo.
Il Sole osservato
è ampio circa 0,5°,
un angolo piccolo, allora vale l’approssimazione che l’ampiezza
del Sole è
inversamente proporzionale alla distanza dal punto di osservazione ( più
grande, più vicino ).
Abbiamo, pertanto, in
modo proporzionale ( i cm misurati ), il valore
della distanza massima
e quello della distanza minima.
Usando le proprietà geometriche dell’ellisse ( che sia tale lo dice
la 1° legge di Keplero ), possiamo calcolare l’eccentricità
( parametro dimensionale e pertanto indipendente dalle unità di
misura: vanno benissimo i cm del Sole proiettato ).
Supponiamo di aver misurato:
diametro massimo al 3
gennaio ( Perielio
) = 10,00 cm
diametro minimo al 4
luglio ( Afelio
) = 9,67 cm
allora possiamo calcolare:
valore medio del diametro del Sole
= 9,84 cm
eccentricità dell’orbita del Sole
attorno alla Terra
( o che è lo stesso, eccentricità dell’orbita della Terra
attorno al Sole
) =
= eccentricità
= ( 10 / 9,84 ) - 1
= 0,0167
z |
z
Dimensionamento dell'orbita
Terra-Sole
image credit Perseus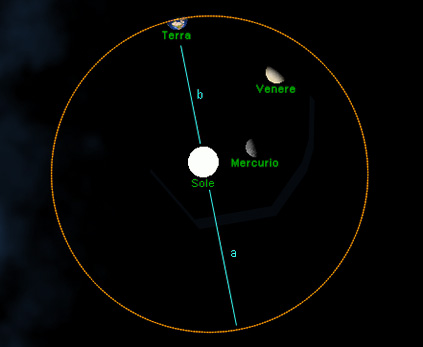 image
credit Perseus image
credit Perseus |
conosciamo il valore delle seguenti
grandezze: Unità Astronomica UA
( 149.597.870,691 km
) - Eccentricità Orbita
Terrestre ( 0,0167
)
sappiamo che la distanza
media Terra-Sole vale 1,00000011
• UA = 149.597.887,147
= d
calcoliamo:
a ( maggiore
) = d • (
1 + 0,0167 ) = 152.096.171,862
- b
( minore ) = d
• ( 1 – 0,0167 )
= 147.099.602,431
z
"Giorno
solare medio" - definizione
|
L’osservazione del Sole
alla meridiana ( “Sole
vero” o “Sole
osservato” o “Sole
fisico” )
ci mostra in modo inconfutabile che il tempo scandito, detto anche “tempo
vero” non
fluisce in modo costante durante l’anno. Nell’arco dell’anno, in altre
parole, i giorni non hanno durata eguale.
Fin dall’antichità ( Ipparco
e Tolomeo
) si era capito che un “metronomo
irregolare” mal
si adattava per fare di conto sul moto dei pianeti.
Essi inventarono pertanto il “Sole
medio”, un Sole
non esistente nella realtà, che fluisce
in modo uniforme nel cielo.
Bisogna però che il “Sole medio”
rispetti una quantità di vincoli per essere utile. Vediamo nel seguito
i passaggi logici, che richiedono l’ausilio di due Soli immaginari:
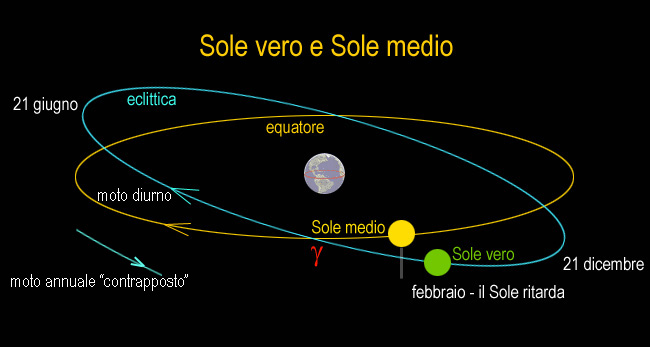
Il Sole fittizio
o dinamico è un astro immaginario
che percorre con moto uniforme l’eclittica,
passando insieme col Sole vero
al
Perigeo e
all’Apogeo.
Il Sole medio
è un astro immaginario che percorre
con moto uniforme l’equatore: passa al
punto vernale  nello
stesso istante del nello
stesso istante del
Sole fittizio
e vi ritorna (insieme con esso) alla fine di un anno
tropico medio, cioè dopo 365,2422
giorni di 24 ore.
I nostri orologi, meccanici o elettronici,
basati su oscillazioni perfettamente ripetitive, segnano
pertanto il tempo scandito dal “Sole medio”
detto "tempo
medio", ovvero
dicono che ogni giorno ha una durata di
24 ore.
Questa può essere considerata un’opportuna
media della durata dei giorni nell'arco di un anno.
z
z
"Giorno
solare medio" - definizione
- image
credit Pighin
il “Sole
vero” o “Sole
osservato” o “Sole
fisico”
scorre annualmente con le regole della
2^ legge di Keplero
sull'eclittica
...
il "Sole
medio"
scorre annualmente con moto
uniforme lungo l'equatore
celeste ... essi coincidono
in quattro momenti dell'anno ...
la "sfera
celeste"
ruota giornalmente con moto uniforme
attorno alla Terra,
originando il "giorno
solare vero"
e il "giorno
solare medio" |
| durata
del "giorno istantaneo vero"
- una paginetta di formule
image credit Pighin  image credit Pighin
image credit Pighin
sommando algebricamente
le variazioni giorno per giorno ottengo gli anticipi
e i ritardi rispetto al "giorno
medio"
z |
z |
z
anticipi e ritardi sul "Tempo
solare medio" a causa dell’eccentricità
dell'orbita
image credit Perse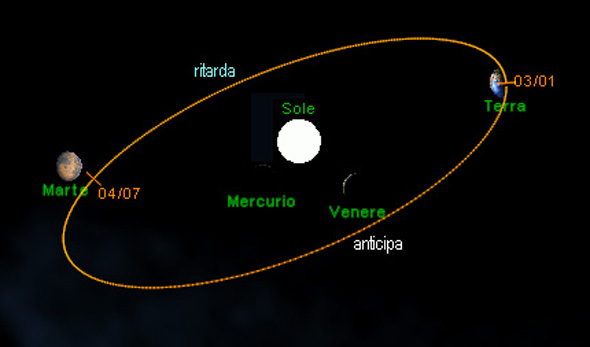 image credit Perseus
image credit Perseus
|
A causa dell'eccentricità
dell'orbita della Terra
essa viaggia con velocità non costante e il Sole
vero, pertanto,
ritarda o anticipa ...
Ciò avviene secondo la linea
degli apsidi ... al Perielio
e all'Afelio
lo scostamento è nullo,
mentre nei periodi intermedi il Sole
alternativamente ritarda e anticipa.
.
anticipi
e ritardi sul "Tempo solare medio"
a causa dell’eccentricità dell'orbita
image credit Perseus 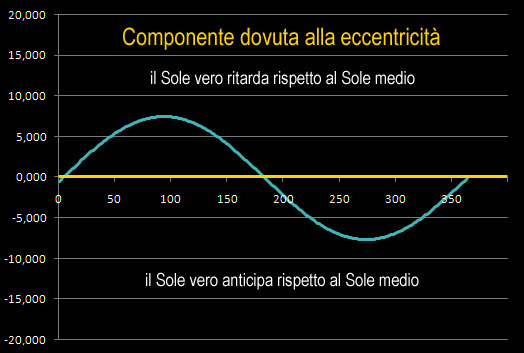 image credit Pighin
image credit Pighin
Il periodo della componente di anticipo/ritardo
dovuta alla eccentricità è annuale
....
|
.
| z
anticipi e ritardi sul "Tempo
solare medio" a causa dell’asse
inclinato di rotazione
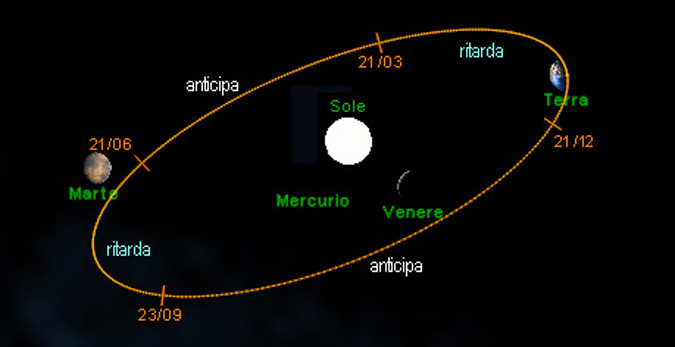
image credit Perseus
|
A causa dell'inclinazione
dell'asse di rotazione inerziale della
Terra
rispetto all'eclittica ( piano orbitale Terra-Sole
) il Sole
ritarda o anticipa
Ciò avviene con
cadenza stagionale ... all'inizio della
stagione lo scostamento è nullo
( quarti di orbita
), mentre nei periodi intermedi si hanno
alternativamente ritardi e anticipi
( ottavi di orbita
).
.
| anticipi
e ritardi sul "Tempo solare medio"
a causa dell’asse inclinato di rotazione |
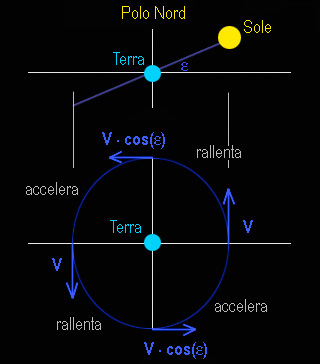 |
In una visione geocentrica il Sole
rivoluziona in un anno attorno alla Terra.
La sua orbita è inclinata di un angolo  = 23° 26' 21,448'' [ anno 2000 - Effemeridi Nautiche IIM ].
= 23° 26' 21,448'' [ anno 2000 - Effemeridi Nautiche IIM ].
La velocità del Sole
al solstizio d'estate ( in
alto ) e al
solstizio d'inverno ( in
basso ) è
parallela al piano equatoriale. Pertanto,
proiettata su di esso, vale V.
La velocità del Sole
agli equinozi è inclinata di  .
Pertanto, proiettata sul piano equatoriale,
vale V cos( .
Pertanto, proiettata sul piano equatoriale,
vale V cos( )
[ minore di V
]. )
[ minore di V
].
Un abitante della Terra ( longitudune e latitudine
fissata ) vedrà dei rallentamenti e degli anticipi con
cadenza stagionale ... se all'inizio della
stagione si passa, ad esempio, da ritardo ad anticipo, in quel punto l'anticipo
[ ritardo ] sarà nullo.
In buona sostanza, si avrà un andamento
sinusoidale che avrà un passaggio per
lo zero ad ogni inizio di stagione.
Il ritado [ anticipo ] accumulato agli ottavi
raggiunge il valore massimo di 9,87
minuti. |
.
anticipi
e ritardi sul "Tempo solare medio"
a causa dell’asse inclinato di rotazione
image credit Perseus 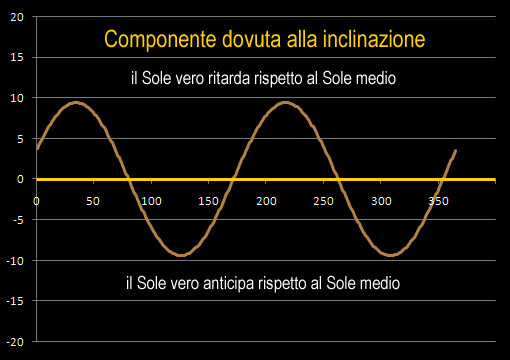 image credit Pighin
image credit Pighin
Il periodo della componente di anticipo/ritardo
dovuta all'asse inclinato di rotazione inerziale è semi-annuale
....
|
.
| z
composizione di anticipi e
ritardi sul "Tempo solare medio"
image credit Perseus 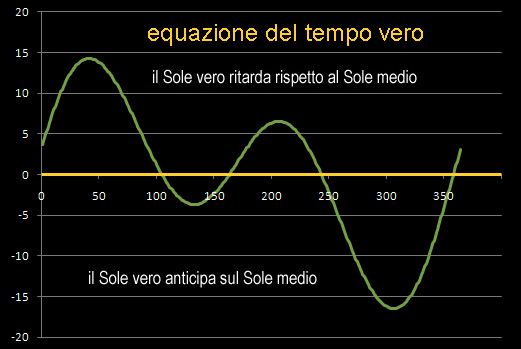 image credit Pighin
image credit Pighin
|
La combinazione dei contributi dovuti alla "inclinazione
dell'asse di rotazione"
e quelli dovuti alla "eccentricità
dell'orbita"
dà origine ad un grafico risultante
denomonato "Equazione del tempo vero".
Normalmente esso esprime la correzione
in minuti del "mezzogiorno vero"
rispetto al "mezzogiorno medio"
... coincidono con gli anticipi e ritardi della "culminazione"
del "Sole osservato".
.
| zz
il "Giorno
solare vero" misurato: l'orologio
solare equatoriale |
z
image credit Sandro
Arpe  image credit Sandro Arpe
image credit Sandro Arpe |
|
z
La "cadenza
diurna",
misurabile tra due
culminazioni successive con la meridiana,
varia continuamente da
z
un minimo di 23h 59m 39s
(a cavallo del 16 settembre)
meno 21
secondi
z
un massimo di 24h 00m 30s
(a cavallo del 23 dicembre )
più 30
secondi |
zz |
z
z
correzioni da apportare alla
"meridiana" per
passare dal "tempo vero"
al "tempo medio"
 zz zz image credit Sandro Arpe
image credit Sandro Arpe
|
 |
correzione
della ora solare estiva
correzione della longitudine
correzione della equazione
del tempo |
( per
l'Italia + 1 ora, se in vigore )
( per il Tigullio
+ 23 minuti rispetto al meridiano 15° dell'Etna
)
( funzione della
data, può essere negativa o positiva
)zz |
|