 |
| "Risonanze
rotazione-rivoluzione" introduzione ... |
z
Nel sistema solare è cosa comune trovare
rapporti semplici
( 1/1, 3/2,
2/1, 5/2,
3/1, 4/1
) tra vari tipi di periodicità.
Il caso più eclatante, che tutti noi conosciamo,
è quello della Luna
che ci mostra sempre la stessa faccia.
Detto in termini astronomici ciò significa che il suo periodo
di rivoluzione (27,3 giorni)
è uguale al suo periodo di rotazione (27,3
giorni).
Il giorno lunare, quindi, dura quasi un mese. Questa uguaglianza si esprime
in modo sintetico dicendo che la Luna è in risonanza
rotazione-orbita 1:1 attorno alla Terra.
Un altro caso molto famoso tra gli appassionati
è quello di Mercurio
che compie tre rotazioni in due rivoluzioni.
Detto in termini astronomici ciò significa che il suo periodo
di rivoluzione (87,969 giorni)
è pari a 3/2
del suo periodo di rotazione (58,6462 giorni).
Per effetto combinato della rotazione intrinseca costante e di quella variabile
periodicamente imposta dall'orbita, il
giorno mercuriano (giorno sinodico)
dura 115,88 giorni.
Questo rapporto fisso si esprime in modo sintetico
dicendo che Mercurio
è in risonanza rotazione-orbita
3:2 attorno al Sole.
Questa risonanza appare contro-intuitiva,
tanto è vero che, all'inizio del secolo XIX, Bessel
(1813)
aveva dedotto da disegni della superficie una rotazione di 24h
0m 53s. Questa convinzione fu discreditata
in modo definitivo da Schiaparelli
(1889)
che, sulla base di una serie di osservazioni, convinse la comunità
scientifica che la rotazione avveniva in 88
giorni. Fu questo un grosso passo avanti
nel pensare ad una rotazione molto lenta ...
Addirittura Dollfus
(1953),
comparando i disegni di Schiaparelli con i suoi, aveva concluso per una
risonanza 1:1, quindi 88 giorni,
« con
una precisione migliore di una parte su diecimila ».
Solo osservazioni radar recenti di Pettengill
e Dyce (1965)
hanno condotto ad una rotazione diretta di 59±5
giorni.
z
Tutto questo saggio è ispirato
all'articolo "The Rotation of the Planet Mercury"
di Bepi Colombo
e Irwin I. Shapiro
z |
| "Una
simpatica nota storica" - il pensiero astronomico
prima del 1965
... |
z
Conoscere
– Grande enciclopedia di cultura generale documentata completamente con
illustrazioni a colori
Volume I – Fratelli Fabbri Editori - 1962
- pagine 30-31
Mercurio
È il pianeta più piccolo, più
veloce e più vicino al Sole (ne dista 58 milioni di km). Gli
gira attorno in 88 giorni, mostrandogli sempre
la stessa faccia. Impiega
88 giorni a completare
un giro su sé stesso. Per questo,
la parte sempre rivolta verso il Sole è un deserto di rocce incandescenti,
con una temperatura di 400 gradi sopra lo zero. Mercurio non ha atmosfera
né vita. Diametro: km 4800. gira intorno al Sole alla velocità
di 48 km/s.
Venere
Dopo Mercurio,
è il pianeta più vicino al Sole
(108 milioni di chilometri). Gli gira attorno
in 225 giorni, compiendo un giro su sé
stesso in 30 giorni circa. È completamente
avvolto da immense nubi di polvere. È di pochissimo più piccolo
della Terra: il suo diametro misura km 12300, mentre quello della Terra
12756. Gira intorno al Sole alla velocità di km 35 al secondo. Non
ha né atmosfera né vita.
Plutone
È il pianeta più lontano dal Sole;
gli gira intorno a 5919 milioni di chilometri di distanza, impiegando 248
anni per compiere ogni giro. Non si sa bene come sia composto; probabilmente,
per la temperatura bassissima (230 gradi sotto zero) tutti i gas dovrebbero
essere liquefatti o addirittura solidificati. Non
si sono visti finora suoi satelliti. Diametro
km 6000 circa. Gira attorno al Sole alla velocità di km 4,7 al secondo.
z
z
Nel 1965
si sono fatte scoperte radar epocali - diventano
note le rotazioni di Mercurio
e Venere ...
z |
z
"Risonanze
rotazione-rivoluzione" introduzione ... |
« ...
Bepi Colombo
(1965)
presenta uno studio preliminare, semi-quantitativo per spiegare il periodo
rotazionale di Mercurio.
Egli annota che tale periodo avrebbe potuto essere
esattamente 2/3
del periodo orbitale è dimostrò
che un tale moto rotazionale avrebbe potuto
essere stabile sotto l'influenza di coppie
torcenti da parte del Sole, a patto che
ci fosse una sufficientemente ampia differenza tra i due principali momenti
di inerzia che giacevano nel piano equatoriale
di Mercurio
( i.e. in termini tecnici, a patto che l'elissoide di inerzia di Mercurio
deviasse in modo sufficiente dalla simmetria rotazionale).
Prima di ciò, nel presentare la loro personale
spiegazione mareale della rotazione di Mercurio, Peale
e Gold (1965)
avevano esplicitamente escluso
che una deviazione permanente dalla simmetria assiale avrebbe potuto condurre
ad un periodo rotazionale diverso da quello
di 88 giorni....
... nell'esaminare la nostra analisi preliminare
del modello della interazione di Mercurio
con il Sole,
evidenzieremo possibili percorsi evolutivi che Mercurio avrebbe poturo
seguire e discuteremo su come distinguere tra essi in base a successivi
studi della dinamica del suo moto di rotazione (vedi anche Colombo
e Shapiro
1965)
... ».
Dalle osservazioni radar, alla risonanza ... questo
è il grande passo che compie Bepi
Colombo ... egli, con la sua analisi,
riuscirà a convincere la NASA
a strutturare la missinone Mariner 10
in modo tale da usufruire di questo fenomeno per osservare per ben tre
volte la superficie del pianeta nelle stesse condizioni di illuminazione
e posizione nello spazio ...
L'accuratezza di queste riprese avrebbe consentito
di mettere un punto fermo sulla stabilità di tale rotazione e sulla
presenza di eventuali azioni perturbanti ... L'ipotesi
di lavoro per la dissimetria è molto semplice e concettualmente
risale al pensiero newtoniano del "pianeta oblato" Terra ...
z
"Modello
delle interazioni" Sole-Mercurio |
« ...
La struttura fisica di Mercurio
e la sua forma sono troppo poco conosciute per permetterci di formulare
un modello accurato delle interazioni solari che condizionano il moto rotazionale.
Inoltre, poichè il nostro scopo principale è quello di dimostrare
semplicemente la stabilità di un periodo rotazionale uguale a due
terzi del periodo orbitale, limiteremo la nostra analisi ad un modello
molto semplice.
Anzitutto, considereremo che il
vettore velocità angolare di Mercurio
sia perpendicolare al suo piano orbitale,
in modo da ridurci ad un problema a due dimensioni.
Assumiamo che la coppia totale esercitata su Mercurio
dal Sole sia composta da due parti:
-
• una coppia mareale
( il bulbo mareale si ha in quanto il pianeta
è deformabile )
-
• una coppia di quadrupolo
( presente se la distribuzione di massa
sul piano equatoriale non è simmetrica
)
[ tutti i corpi celesti sono deformabili ed hanno
qualche asimmetria, più o meno pronunciata ] ... come rappresentare
ciò analiticamente?
Consideriamo dapprima il termine mareale. La teoria
di un oscillatore lineare, debolmente smorzato, mostra che la risposta
è in ritardo di fase rispetto alla funzione forzante per un ammontare
proporzionale al coefficiente di smorzamento. Nel nostro caso, l’analogo
del coefficiente smorzante potrebbe dipendere dalla intensità e
dalla frequenza della funzione forzante come pure dalle proprietà
strutturali e di composizione del pianeta
... ».
| z
La "coppia
mareale" Sole-Mercurio |
Affinché sia stabile
il moto di rotazione, si richiede che sia
nulla la coppia media
( mareale + quadrupolo
), e che, se l’orientazione di Mercurio
e la frequenza di rotazione sono perturbate, allora la coppia risultante
tenda ad opporsi a queste perturbazioni ... 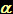 è molto piccolo ...
è molto piccolo ...
... se il pianeta fosse indeformabile, allora 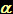 = 0 ... la coppia mareale sarebbe sempre
nulla ... calcoli tediosi conducono a:
= 0 ... la coppia mareale sarebbe sempre
nulla ... calcoli tediosi conducono a:
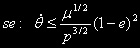 z z
z z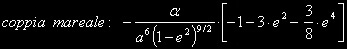
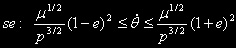

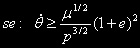 z z
z z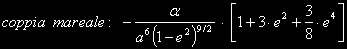
questa è una funzione regolare ( una
volta fissata la eccentricità e
) che da un valore massimo costante passa con regolarità ad un valore
minimo ... essa deve bilanciarsi con la
coppia di quadrupolo ( quella
dovuta alla asimmetria di minimo momento d'inerzia
) ...
| z
La "coppia
mareale" Sole-Mercurio e Terra-Luna |
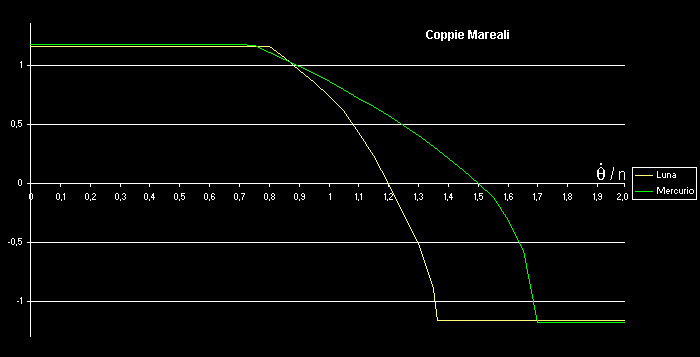
L'andamento di queste "coppie" è continuo,
anche se non uniformemente derivabile |
z
Sole-Mercurio - "il
momento di quadrupolo" |
z
« ...
Possiamo trattare per semplicità la permanente asimmetria assiale
di Mercurio
come un dipolo nel piano equatoriale, sovrapposto al pianeta sferico. Se
il dipolo consiste di due punti di massa m,
ciascuno distante d
dal centro di massa del pianeta, con una linea congiungente che passa per
il centro di massa, allora [ la risultante
distribuzione di massa avrà andamento ellittico
] ... »
| z
La "coppia
di quadrupolo" Sole-Mercurio |
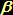 e e  sono molto piccoli ... se la distribuzione di massa fosse uniforme,
sono molto piccoli ... se la distribuzione di massa fosse uniforme, 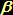 = 0 e
la coppia di quadrupolo sarebbe sempre nulla ... con calcoli tediosi:
= 0 e
la coppia di quadrupolo sarebbe sempre nulla ... con calcoli tediosi:
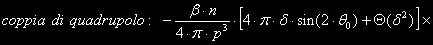
z
z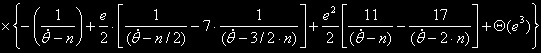 dove
dove 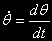
il primo fattore si annulla per 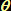 0
= 0° o per 0
= 0° o per 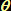 0
= 180° diventa infinitesimo quando 0
= 180° diventa infinitesimo quando 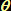 0
---> 0° o 0
---> 0° o 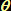 0
---> 180°; pertanto può controbilanciare
i punti di singolarità all'infinito del secondo fattore in parentesi
graffe ... quest'ultimo mostra dei poli per 0
---> 180°; pertanto può controbilanciare
i punti di singolarità all'infinito del secondo fattore in parentesi
graffe ... quest'ultimo mostra dei poli per 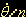 intero o semi-intero, cioè per esempio:
intero o semi-intero, cioè per esempio:  = n,
= n,
 = n/2,
= n/2,  = (3/2)•n,
= (3/2)•n,  = 2•n ...
= 2•n ...
il gioco dei coefficienti, di cui la maggior parte
dipende da e
o sue potenze, è tale per cui a bassi valori di e
prevale la risonanza  = n, mentre per valori alti di e
prevale la risonanza
= n, mentre per valori alti di e
prevale la risonanza  = (3/2)•n ... ecco il motivo della risonanza
rotazione-orbita di Mercurio
...
= (3/2)•n ... ecco il motivo della risonanza
rotazione-orbita di Mercurio
...
il caso di eccentricità bassa corrisponde
alla situazione Terra-Luna,
mentre il caso di eccentricità alta corrisponde alla situazione
Mercurio-Sole....
z
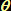 0
assume alla risonanza uno scostamento infinitesimo rispetto a 0°
o 180°,
in concreto un angolo nullo o piatto ... 0
assume alla risonanza uno scostamento infinitesimo rispetto a 0°
o 180°,
in concreto un angolo nullo o piatto ... 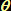 0
è l’orientazione dell’asse equatoriale
di minimo momento d’inerzia rispetto alla linea degli apsidi al perielio
... 0
è l’orientazione dell’asse equatoriale
di minimo momento d’inerzia rispetto alla linea degli apsidi al perielio
...
| z
Lo "equilibrio
delle coppie" nel sistema Sole-Mercurio |
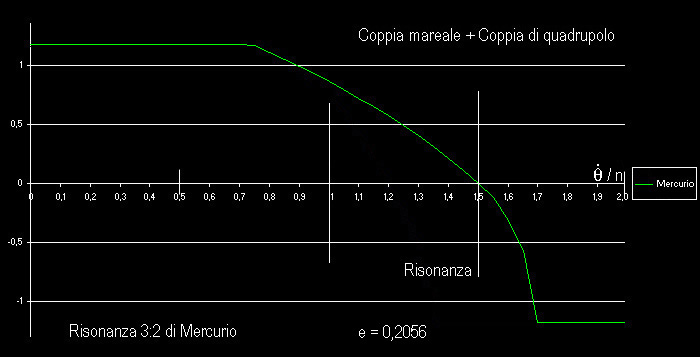
La coppia di quadrupolo nel punto 1:1, pur avendo
ampiezza simile a quella in 3:2, non bilancia mai la coppia mareale
Il grafico della coppia di quadrupolo non è
in scala - deve avere ampiezza tale da bilanciare la coppia mareale alla
risonanza |
| z
La "risonanza
3:2" nel sistema Sole-Mercurio |
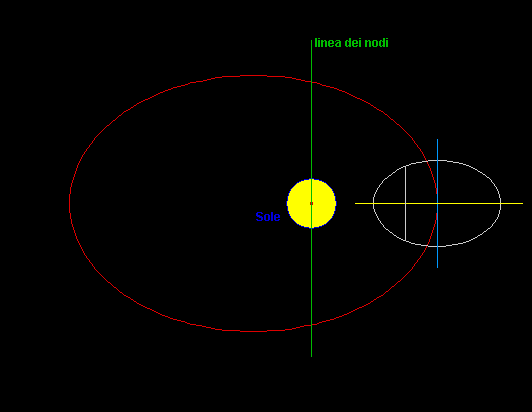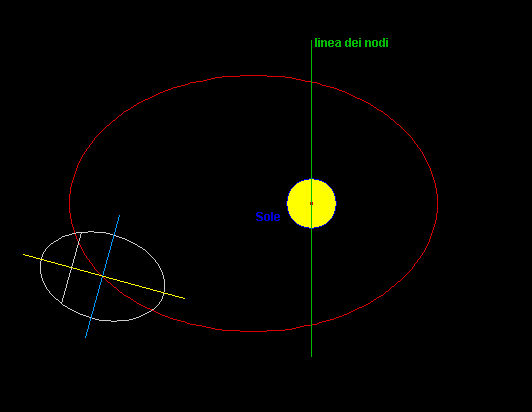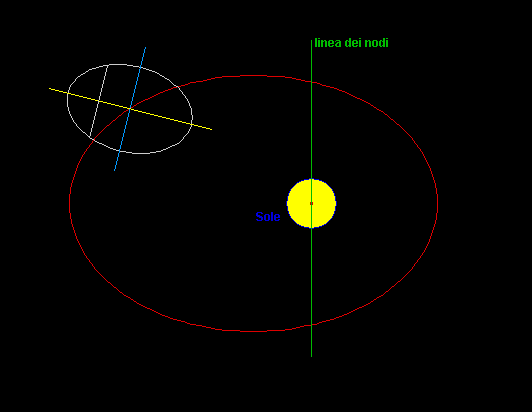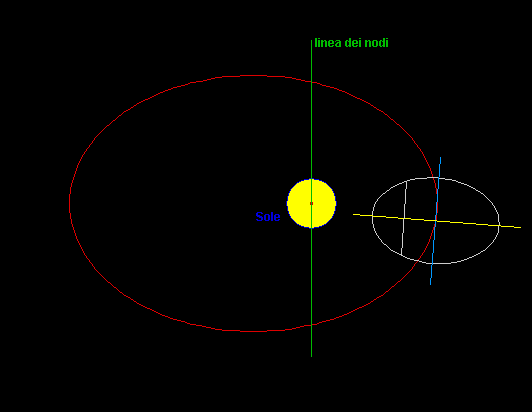
L'asse giallo
della distribuzione di massa, che qui rappresenta Mercurio,
è la direzione del minimo momento
d'inerzia ...
la marea di Mercurio
è sempre diretta verso il Sole
- l'asse giallo
è sempre diretto verso il Sole
al Perielio
(  0
= 0° o
180° ) ... 0
= 0° o
180° ) ... |
| z
Lo "equilibrio
delle coppie" nel sistema Terra-Luna |
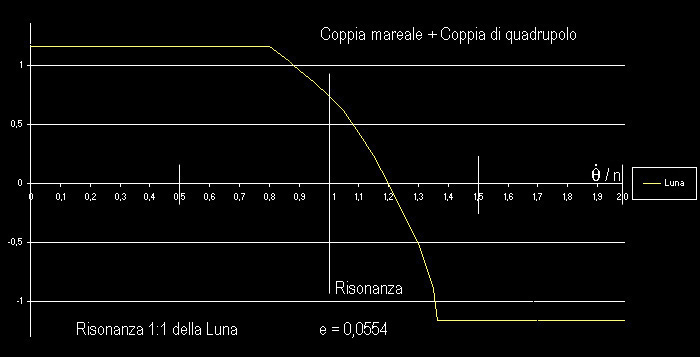
La coppia di quadrupolo nel punto 3:2, di ampiezza
molto minore di quella in 1:1, non bilancia mai la coppia mareale
Il grafico della coppia di quadrupolo non è
in scala - deve avere ampiezza tale da bilanciare la coppia mareale alla
risonanza |
| z
La rotazione
della Luna è "frenata
marealmente" fino a che ci mostra la stessa
faccia
Il risultato del processo è una "risonanza
rotazione-orbita 1:1"
( rotazione
= rivoluzione
= 27,3 giorni
) |
z
| z
Per chi non riesce a credere
che la Luna ruoti su sé stessa ...
portando a zero il raggio orbitale ( "esperimento
mentale"
), si elimina il moto di rivoluzione: rimane
solo la rotazione ... |
|