z 
Albert nasce a Ulma, in Germania, il 14 marzo 1879, da padre, Hermann, e madre, Pauline Kock, ebrei non praticanti. Nel 1880 l’impresa familiare verte in difficoltà, e l'intera famiglia si sposta a Monaco, dove il padre apre, col fratello Jacob, ingegnere, una piccola fabbrica. Un anno dopo nascerà la sorella Maja. Albert impara a parlare molto tardi, e la sorella ci dice: “Pronunciava ogni frase lentamente e usava ripeterla più volte a fior di labbra” aggiungendo, si direbbe col senno di poi, “Si manifestava in un modo curioso la precoce profondità del suo pensiero”. (1)  

Ben presto il piccolo Einstein si rivela curioso e pronto nell'apprendimento. Sarà Albert stesso a ricordare un episodio avvenuto all'età di cinque anni, - quando riceve in dono dal padre una bussola, ed entusiasta rimane colpito dal movimento dell'ago, influenzato da un campo magnetico invisibile- come motivo che, probabilmente, lo spinge a studiare più tardi il campo gravitazionale.  

Nel 1888 comincia a frequentare il Luitpold Gymnasium, una scuola media superiore di Monaco, che oggi porta il suo nome, e a causa della quale sviluppa una profonda avversione verso atteggiamenti oppressivi e autoritari, che lo portarono a rinunciare alla cittadinanza tedesca chiedendo quella svizzera.  

La famiglia per il giovane rappresenta un rifugio sicuro, oltreché un impareggiabile punto di stimolo e di studio. Grazie allo zio Jacob comincia in età precoce lo studio dell'algebra. Impara la geometria e, a soli quindici anni, lo studio infinitesimale, mentre dalla madre viene stimolata la sua vena artistica con lo studio del violino, che diverrà una passione mantenuta per il resto della vita.  

La sua sensibilità e la sua vivacità intellettuale vengono ben sollecitate da una famiglia di ampie vedute, la cui elasticità mentale però non ritrova nell'ambiente scolastico, né nei metodi educativi allora applicati. Osteggia lo studio mnemonico e pedissequo, perché ritiene non permetta la piena comprensione delle materie e renda noioso l'apprendimento, uccidendo la curiosità dell'allievo e critica aspramente i metodi brutali che uccidono la personalità, minano la fiducia nel prossimo e formano un individuo sottomesso.  

(1) Silvio Bergia – I grandi della scienza n° 6 – Einstein – in Le Scienze 
 
 
 
 
 
 
 
 
 
 
 

  
Sarà per questi motivi che non riuscirà a conseguire il diploma di scuola secondaria, obbligandolo a iscriversi alla scuola cantonale svizzera di Aarau, della quale conserverà invece un ottimo ricordo.  

La successiva frequenza del politecnico fa invece maturare in lui la consapevolezza di dedicarsi allo studio della fisica e non dell'ingegneria.  

Il fisico Heinrich Weber gli dirà: “Lei è intelligente, Einstein, estremamente intelligente, ma ha un gran difetto: non vuole lasciarsi insegnare una sola cosa! ” (2)  

La formazione che ha in seno alla famiglia influenza anche la sua visione religiosa e spirituale, permettendogli di sviluppare un sua personale visione, che viene determinata dagli studi conseguiti.  

Nessun credo settario, nessuna dottrina, né l'idea di un “Dio antropologico” (3), ma il riconoscimento nella natura di un ordine e di un disegno costituiscono la peculiarità del suo pensiero in questo ambito: “Il sentimento religioso provocato dalla comprensione delle profonde interrelazioni della realtà è un qualcosa di diverso da quello che di solito viene definito con il termine religioso. È più propriamente un sentimento di venerazione per il disegno che si manifesta nell'universo materiale. Non ci porta ad immaginare un essere divino a nostra immagine e somiglianza, che ci fa domande e che si interessa a noi come individui. Non esiste né volontà, né dovere ma solo essere assoluto. ” (4)  

(2) Silvio Bergia – I grandi della scienza n° 6 – Einstein – in Le Scienze 
(3) Helen Dukas and Banesh Hoffman, Albert Einstein – The Human Side, Princeton University Press, 1979 
(4) Ibidem 
 
 
 
 
 
 
 
 

z 
Uno dei primi argomenti da analizzare in profondità sarà quello del mezzo che consente alle onde elettromagnetiche ( Maxwell ) di propagarsi. Storicamente esso è stato denominato “etere”. Molti ne hanno analizzato le proprietà arrivando spesso a conclusioni inusitate sulla rigidità necessaria a spiegare i fenomeni fisici. Ormai era assodato il moto di rivoluzione del pianeta Terra attorno al Sole (James Bradley 1729). La domanda sorgeva spontanea: l’etere era trascinato dalla Terra o essa lo attraversava causando così un "vento di etere" che doveva mostrare conseguenze fisiche? Un’altra cosa era certa, a partire dalle equazioni di Maxwell, e cioè che la luce si propaga in questo etere ad una velocità costante che dipende da due grandezze fisiche dello stesso (costante dielettrica e permeabilità magnetica).  

dove le quantità a denominatore sono misurabili fisicamente.  

La domanda era se il moto dell’etere, rispetto alla Terra, causasse o meno variazioni della velocità della luce misurabili (essendo la velocità della luce nell’etere ormai stabilita).  

Molti furono gli esperimenti di dubbia interpretazione, data la piccolezza del fenomeno, il cui valore era stato stimato proporzionale a . Infine fu dimostrato che, in qualunque direzione si misurasse, la velocità della luce era invariabile. In particolare, grazie all'esperimento di Michelson-Morley, fu dimostrato che la velocità della luce è costante in tutte le direzioni, indipendentemente dal moto della Terra, non risentendo così del cosiddetto vento di etere.  
 

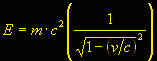
 z 

Era dunque necessario trovare una formula di passaggio da un sistema fermo rispetto all’etere, ad uno invece in moto, che rendesse comunque ragione di questa invarianza della velocità della luce. 

La prima proposta venne da due studiosi, Fitzgerald e Lorentz, che assunsero, per un corpo in moto attraverso l’etere, una sorta di “contrazione" delle dimensioni, che faceva tornare i conti.  

La contrazione era data dal fattore  (qui c’è in embrione la relatività ristretta RR).  

Inizialmente questo sembrava un espediente puramente matematico per far tornare i conti, ma la comunità scientifica lo accolse con un certo entusiasmo.  
 
 
 
 
 
 
 
 
 
 

 z 
La fisica newtoniana si basa sul concetto elementare astratto di punto materiale, o particella, quindi la materia è considerata discontinua a priori. È noto come Newton sia stato un grande fautore della teoria corpuscolare della luce.  
 

Come si spiegano i fenomeni meccanici nell’ambito di questo contesto? È ipotizzata la “azione a distanza” tra punti materiali, con effetto immediato.  
 

Dato un corpo sferico, la sua azione diminuisce in modo inverso al quadrato della distanza. Ciò naturalmente porterebbe ad una azione infinita tra due punti a contatto, cioè a distanza nulla. Su questa incongruenza non ci si sofferma però agli esordi della gravitazione universale.  
 

Sembrava ormai che il metodo di Newton potesse dare risposta a tutta la meccanica.  
 

Un problema sorse, però, quando, nella seconda metà del XIX secolo, divennero note le leggi della elettrodinamica di Maxwell. Esse, infatti, non potevano essere incorporate in maniera soddisfacente nel sistema newtoniano.  
 
 
 
 

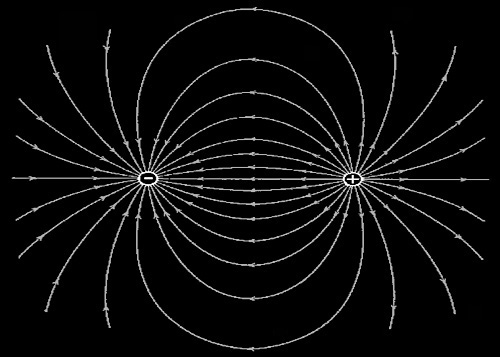
 z 

Maxwell determinò nel dettaglio queste leggi che trovano la loro espressione naturale nelle equazioni differenziali per i campi elettrico e magnetico. In particolare si riscontra che l’onda elettromagnetica si deve propagare con una velocità costante e finita, il cui valore è fornito dalla misura di grandezze caratteristiche dell’ambiente circostante.

Il campo è una realtà misurabile che “abita” nello spazio circostante, capace di interagire con i corpi che in esso si trovano. Esso è dotato di una struttura definibile topologicamente e dipende dalla geometria delle sorgenti e da quella dei corpi “illuminati” da esso. Nel pensiero di Maxwell c’è posto per l’etere. 

Per studiare la struttura di un campo viene molto bene la astrazione di una “particella di prova” infinitesima, tale cioè da risentire della azione del campo, ma piccola quanto basta da non perturbarlo. Spesso il campo è rappresentato mediante “linee di forza”, cioè quelle linee lungo le quali si muoverebbe la particella di prova se lasciata libera.  

Vediamo come si può visualizzare in pratica un campo magnetico: si dispone su un piano un magnete permanente, si sparge minuta limatura di ferro, sensibile ad esso, e si danno piccoli colpetti al piano per permettere un inizio di moto delle particelle. Esse disegneranno l’andamento delle linee di forza del campo, come da fotografia seguente.  
 
 

La sensazione di “qualcosa che permea lo spazio”, capace di agire in concreto, è davvero immediata! La limatura di ferro è sufficientemente minuta da perturbare in modo trascurabile il campo.  
 
 
 
 
 
 
 
 

z 
Römer ha misurato con metodo astronomico la velocità finita della luce, il lavoro di Maxwell ritrova proprio quel valore per la propagazione delle onde elettromagnetiche. Il suo campo è completamente determinato da processi contigui espressi da equazioni differenziali, matematicamente “continue” nella funzione, nelle derivate prime e seconde almeno.

L’elettrodinamica di Maxwell ha anche punti deboli, ammette infatti singolarità (ad esempio a contatto delle due cariche) che si traducono in valori infiniti della funzione. 

Forse il pensiero di Cartesio (uno spazio tutto pieno) non era così lontano dalla realtà. I suoi vortici si sono concretizzati nelle linee di campo di Faraday, su di esse inoltre si riesce a fare di conto. Quando accendiamo il condizionatore abbiamo per un breve periodo un assorbimento enorme, è la “corrente di spunto”, necessaria per riempire lo spazio dei motori di campo magnetico, senza quello non ci può essere l’energia meccanica richiesta (pompa di calore).

Einstein amplia e meglio definisce il “campo” – senza “energia” lo spazio non esiste

Einstein fa suo il concetto di campo e ne approfondisce le proprietà. Lo spazio ora propriamente esiste solo se ci sono masse che fanno campo, al di fuori di quest’ultimo non esiste nulla, la massa crea il campo, il campo agisce sulla massa stessa.

In questo senso è assunto anche il il principio di Mach, una ipotesi formulata nel 1893, che afferma:  

L'inerzia di ogni sistema è il risultato dell'interazione del sistema stesso con il resto dell'universo. In altre parole, ogni particella presente nel cosmo ha influenza su ogni altra particella.  

Essendo la relatività assunta nel contino, l’approfondimento delle conseguenze ha portato alla esistenza di singolarità, i famosissimi “buchi neri”, in cui la funzione va all’infinito. Per superare questo scoglio (tutto il mondo della energia nucleare ce lo conferma) basta pensare la materia come discretizzata (Plank), anche la relatività generale non è quindi una teoria completa.  

La meccanica quantistica oggi è ancora troppo farraginosa per applicarla con facilità a sistemi di grandi dimensioni (e.g. galassie). Essa si presta bene per il molto piccolo o per strutture soggette a pressioni enormi (e.g. stelle di neutroni), dove la meccanica classica o la relatività non hanno risposte. Da tempo gli studiosi tentano di fare una grande sintesi con una teoria unificata, ma ad oggi la meta appare ancora molto lontana.   
 
 
 
 
 
 
 
 
 
 
 
 

z 
La relatività ristretta (o relatività speciale), fu la prima ad essere presentata da Einstein, con l'articolo Zur Elektrodynamik bewegter Körper (Elettrodinamica dei corpi in movimento) del 1905, per conciliare il principio di relatività con le equazioni delle onde elettromagnetiche.  

La teoria di Einstein scarta del tutto il concetto di etere, oggi non più utilizzato. I postulati della relatività ristretta si possono così enunciare:  

primo postulato (principio di relatività): tutte le leggi fisiche sono le stesse in tutti i sistemi di riferimento inerziali;  

secondo postulato (invarianza della luce): la velocità della luce nel vuoto ha lo stesso valore in tutti i sistemi di riferimento inerziali, indipendentemente dalla velocità dell'osservatore o dalla velocità della sorgente di luce.  

Le trasformazioni di Lorentz soddisfano il secondo postulato: se per un osservatore in un sistema di riferimento inerziale la velocità della luce è c, tale sarà per un qualunque altro osservatore in un sistema di riferimento inerziale in movimento rispetto al proprio.  

Le leggi dell'elettromagnetismo, nella forma dell'elettrodinamica classica, non cambiano sotto le trasformazioni di Lorentz, e quindi soddisfano il principio di relatività. Einstein, in particolare, trovò la legge che esprime l’energia di un corpo di massa m, che vale per ogni riferimento inerziale:  

che nella formulazione completa di Einstein diventa   
 
 
 
 
 
 
 
 

z 
E' quindi facile capire come massa ed energia si equivalgano e come esse siano due facce della stessa medaglia. In sostanza la massa è una forma di energia estremamente concentrata: essa scompare quando compare energia e viceversa. In particolare, se un corpo assorbe una quantità di energia, la sua massa non si conserva ma aumenta; viceversa la massa del corpo diminuisce se perde energia, per esempio emettendo luce.  

La teoria della relatività ci fornisce, quindi, un’altra sorpresa: poiché la massa non è altro che una forma di energia, essa non si conserva separatamente, ma si aggiunge all’energia cinetica e all’energia potenziale nell’enunciare la conservazione dell’energia meccanica.  

L'enorme fattore di conversione che lega la massa e l'energia spiega come, concentrando un grosso quantitativo di energia, si possa creare una piccola quantità di materia e anche come, partendo da una piccolissima massa, si possa ottenere molta energia. La conversione di un chilogrammo di materia (equivalente a 25 miliardi di Kilowattora) coprirebbe, in pratica, il consumo mensile di energia elettrica in Italia (dato per anno 2004).  

Einstein non si è dunque fermato alla semplice relazione di Lorentz, ma ne ha scavato tutte le possibili implicazioni, giungendo ad una sintesi formidabile: il creato non è null’altro che una manifestazione variata di un unico ente, cioè l’energia (la luce, le reazioni chimiche, energia cinetica, energia potenziale, energia atomica, massa).  
 
 
 
 
 
 
 
 
 

z 
In un sistema legato l'energia si mantiene ad un livello inferiore rispetto a quella degli elementi che lo compongono, di conseguenza la sua massa deve essere minore della massa dei componenti. Tale differenza di massa prende il nome di difetto di massa.  

L'energia di legame, indicata con la sigla BE (dall'inglese Binding Energy), è data dal prodotto tra il difetto di massa ed il quadrato della velocità della luce nel vuoto.  

BE = difetto di massa · c²  

Idrogeno H ha peso molecolare = 1,00794 u  
Ossigeno O ha peso molecolare = 15,9994 u  

sembrerebbe dunque che la molecola di acqua H2O debba avere come peso:  

2*1,00794+15,994=18,01528 u in realtà vale 18,015269 u ( difetto di massa )  

in accordo con la legge di conservazione della massa-energia di Albert Einstein. La massa mancante si è trasformata in “energia di legame”, quella necessaria per dissociare H2O negli atomi costituenti. Per l’acqua BE vale, come ordine di grandezza, 10^-5 u, pari a 1,539*10^-18 Joule. 
 
 
 
 
 
 
 

z 

L'energia complessivamente liberata dalla fissione di 1 (uno) nucleo di ²³⁵U è di 211 MeV, una quantità elevatissima data dalla formula:  
 

dove la prima massa è la massa del nucleo di ²³⁵U e del neutrone incidente, la seconda massa è la somma delle masse dei nuclei e dei neutroni prodotti e c è la velocità della luce nel vuoto.  
 

Perciò in questo fenomeno parte della massa iniziale scompare e si trasforma in energia sotto forme diverse.  
 

Circa 11 MeV sono trasportati via dai neutrini emessi al momento della fissione, mentre l'energia effettivamente sfruttabile come energia termica (trasformazione della energia cinetica delle parti prodotte) è di circa 200 MeV per ogni fissione.  
 
 
 
 
 
 
 
 
 
 
 

z 
La teoria della relatività generale o RG venne presentata come serie di letture presso l'Accademia Prussiana delle Scienze, a partire dal 25 novembre 1915, dopo una lunga fase di elaborazione. Esiste un'annosa polemica sulla pubblicazione delle equazioni di campo tra il matematico tedesco David Hilbert ed Einstein; tuttavia, alcuni documenti attribuiscono con una certa sicurezza il primato ad Einstein.  

Il fondamento della relatività generale è l'assunto, noto come principio di equivalenza, che un'accelerazione sia indistinguibile localmente dagli effetti di un campo gravitazionale, e dunque che la massa inerziale sia uguale alla massa gravitazionale.  

Einstein, in realtà, darà al problema dello spazio una risposta ( relatività generale o RG ) che risolve le domande sollevate fin dall’antichità circa il limite dell’universo (cosa vi sarà al di là di tale limite?). Egli ipotizza uno spazio “senza confini”, ma limitato. Il suo è uno spazio-tempo quadri-dimensionale che non è rappresentabile in modo geometrico dalla nostra mente, ma lo è molto facilmente in modo matematico.  

Tuttavia vale la pena di pensare ad una analogia bidimensionale, quella di una superficie di una sfera. Un ipotetico abitante della superficie della sfera è una creatura pari ad un piccolo contorno di superficie sferica. Se la sfera è abbastanza grande, essa apparirà ai suoi abitanti come piatta. Inoltre è "senza confini", nel senso che, comunque esso si muova, rimane sempre sulla superficie e non incontra mai un limite. Al più, può ritornare dopo un giro intero al punto di partenza.  
 
 
 
 
 
 
 

z 
Possiamo visualizzare la superficie della sfera, portandoci in uno spazio con una dimensione in più, cioè uno spazio tridimensionale. Ecco le equazioni:  

una sfera nello spazio tridimensionale  
una sfera nello spazio quadri-dimensionale, come lo spazio-tempo  

Inoltre Einstein, da sempre, aveva sognato un universo “statico”, cioè un universo che visto su larga scala rimane uguale a sé stesso. Un po’ come il geoide, che rappresenta la superficie della Terra. A scala planetaria esso è un’ottima approssimazione. Solo gli abitanti della Terra sono implicati, nella loro vita comune nelle asperità locali dovute alla orografia. Ma può esistere un simile universo? No, almeno nella equazione senza la costante cosmologica, che fa una gravità di segno opposto e potrebbe comunque tenere gonfio l’universo, che, altrimenti, ha solo due possibilità: o si espande o si contrae (può essere statico solo per un attimo al momento della inversione di tendenza).  

Un cielo statico, se non esiste un’impalcatura ideale che lo sorregge, ci cadrà fatalmente sulla testa. L'universo è un modello evolutivo e diventa immediatamente attuale porsi domande circa un “inizio” e una “fine”. (8)  

Quindi la relatività generale di Einstein implica il “Big Bang”. Le equazioni, in quanto operative in modo "continuo" e non "discretizzato", danno in quel punto una singolarità, cioè parametri fisici, come la densità, che assumono valori infiniti. Questo è, ragionevolmente, un limite della RG, che al momento appare solubile solo con una visione quantistica del cosmo. La sintesi tra quanti e RG è “il grande problema” della cosmologia moderna. La RG è rimasta "sopita" per moltissimi anni, soprattutto per il fatto che gli effetti, da essa previsti, erano di entità piccolissima e sembrava che mai avrebbero potuto essere misurati. Ma le moderne tecnologie e l’astrofisica ci forniscono oggi materiale in abbondanza per dare riscontri, favorevoli sinora, alla predizione di questa teoria.  

(8) Silvio Bergia – I grandi della scienza n° 6 – Einstein – in Le Scienze 
 
 
 

z 
Avanzamento del perielio di Mercurio: supera quello dovuto alla meccanica di Newton di 43 secondi d’arco a secolo. Solo la RG dà ragione di questo fenomeno.  

Il caso della rete GPS: il campo gravitazionale della Terra diminuisce allontanandosi dal suo centro. Allora, per un satellite in orbita, due saranno i motivi di variazione del suo orologio.  

Uno: per la RR, essendo in moto rispetto ad un osservatore terrestre, il suo tempo varia  
Due: per la RG, essendo in un campo gravitazionale minore che a terra, il suo tempo varia  

Satelliti di questo tipo sono quelli utilizzati per il sistema GPS. Senza le entrambe correzioni relativistiche, la posizione a Terra sarebbe fornita con errore inaccettabile.  

Il caso della stella di neutroni: (raggio di pochi chilometri e massa simile al Sole). In assenza della RG il limite superiore di massa (oltre il tutto evolve in un buco nero) è pari a 5,7 masse solari. In presenza di RG il limite superiore è di 3,6 masse solari. Qui la RG diventa dunque fondamentale per essere rispondenti alle evidenze osservative.  

Il caso della Pulsar binaria: l’orbita descritta dai due astri ha una separazione dell’ordine di un raggio solare. L’effetto di precessione del periastro è altissimo: più di 4 ( quattro ) gradi all’anno. In particolare la RG prevede per questo caso una consistente perdita di energia sotto forma di onde gravitazionali. L’orbita delle due stelle deve dunque spiraleggiare verso l’interno e il periodo di rivoluzione deve accorciarsi. La predizione teorica di una variazione di 75 microsecondi all’anno è stata confermata nel 1983, in pieno accordo con le previsioni della RG.  
 
 
 
 
 
 
 
 
 

z 
Oggi stanno approntando strumenti per la misura di onde gravitazionali. Sono già state fatte segnalazioni, ma il risultato non è abbastanza discriminato dal rumore di fondo. Nel medio termine anche questa impresa potrà dare un risultato concreto.  

Terminiamo con un po’ di autoironia di Albert su sé stesso: “Certe volte mi domando perché sia stato proprio io a elaborare la teoria della relatività. La ragione, a parer mio, è che normalmente un adulto non si ferma mai a riflettere sui problemi dello spazio e del tempo.   

Queste sono cose a cui si pensa da bambini. Io invece cominciai a riflettere sullo spazio e sul tempo solo dopo essere diventato adulto. Con la sola differenza che studiai il problema più a fondo di quanto possa fare un bambino”. (9)  
  

(9) Ronald W. Clark in Selezione dal Reader's Digest, febbraio 1973