Aforisimi: facciamoci aiutare dagli Psicologi ! - per mestiere frugano nella mente umana

Parole chiave: sistema complesso
Le società tecnologiche hanno un'impronta ecologica drammatica, con conseguente effetto serra, aumento della temperatura media - è solo uno dei molti scenari utilizzabili:

 ♜ fabbriche, produzione di energia, riscaldamento, anticrittogamici, internet, trasporti, causano un
      aumento della temperatura media
 ♜ fondono i ghiacciai, le calotte polari, il che cambia - per esempio - la distribuzione di salinità
      dell'Atlantico, alla lunga si bloccherà la Corrente del Golfo facendo mutare in modo imprevedibile
      il clima dell'Europa
 ♜ l'attuale aumento di temperatura ha riscaldato gli oceani, l'acqua si è dilatata con conseguente
      aumento di qualche cm di livello → molte zone basse hanno ormai le sorgenti salinizzate →
      l'agricoltura non è più possibile

Tutto ciò è stato di fatto imprevedibile, almeno fino ad oggi, con problematiche difficili, risolvibili solo a livello mondiale. Può la scienza aggredire queste problematiche? Questi problemi che includono anche una componente caotica?

 ♜ la risposta è "no", si possono avere solo probabilità di accadimento, non ciò che accadrà realmente
 ♜ le probabilità non si trovano con la sola conoscenza della fisica, ci vogliono computer molto potenti
      che possano tenere conto di tutte le immaginabili retroazioni, molte di esse non ci sono note,
      si tratta di fare modelli, farli girare, modificare finchè non si riesce a far tornare - senza barare - la
      storia passata → a questo punto si può essere fiduciosi di prevedere un po' di futuro
 ♜ il telefonino ci dà ad esempio la probabilità che possa piovere, non la certezza, e non si va oltre
      i 3 giorni → abbiamo capito che la "meteorologia" è un fenomeno complesso
 ♜ le assicurazioni si fanno bastare le probabilità per fare business, questo è un esempio su
      cui riflettere maggiormente ...
 ♜ l'economia è un sistema complesso, chi ha posseduto un'azione sa cosa vuol dire, i grandi investitori
      si affidano ai computer ... ma talora accadono errori irrimediabili
 ,

 Il clima é un sistema complesso:
 " Tutto é relazionato con tutto ! " → una grande
   varietà di comportamenti

Parole chiave: sistema complicato
Pensiamo alla attività della NASA, al progetto Apollo:       un vettore come Saturn V è alto più di 100 metri, pensiamo alle migliaia di subfornitori, al fatto che ciascun particocolare deve combaciare perfettamente con altri di altra provenienza, che non ci possono essere malfunzionamenti altrimenti tutto è fallito, una organizzazione colossale. Eppure si è conclusa felicemente: perché è un sistema complicato, non complesso.

Pensiamo alla posizione della Luna, distante mediamente circa 384.400 km, gli astronomi conoscono la sua posizione con l'approssimazione di un paio di centimetri ! ... il Sestante stesso - una realtà piccola - sa calcolare le eclissi della Luna con la stessa precisione delle Effemeridi Nautiche. Lo schema ci mostra la lunga serie di passaggi, calcoli, soluzione di equazioni, necessari per arrivare al risultato, semplificando si deve calcolare:

 ♜ Tempo siderale a Greenwich, Aberrazione, Nutazione, data della Luna piena, Data giuliana della
      possibile eclisse, Tempo del massimo della possibile eclisse, Tempo del primo e ultimo contatto,
      della penombra, Inizio e fine della penombra
 ♜ se uno di questi dati non c'è - esempio, non esiste l'inizio della penombra - si passa al mese
      successivo, si rifanno i calcoli fino a che non si trova l'eclissi
 ♜ trovata l'eclissi si calcola la proiezione dell'incinazione dell'orbita lunare, la latitudine e la longitudine
      sulla Terra del massimo della eclissi, la distanza della Luna per sapere se sarà anulare
      o no, la longitudine del nodo ascendente, la traduzione di questi valori in pixel per comporre
      il disegno sullo schermo del computer

Alla fine di tutto questo processo, il risultato è garantito - purchè in assenza di errori - perché il moto della Luna è complicato, non complesso.
 ,

 La Luna é un sistema complicato:
 " Moltissimi passaggi seriali ! " - comportamento
   univoco

Parole chiave:
l'orbita della Luna non si ripete maiNel disegno due anni di orbita della Luna, visti dallo spazio:

 ♜ a causa delle molteplici perturbazioni - Terra, Sole, Pianeti, attriti mareali - l'orbita non si richiude, pur
      rimanendo confinata in uno spazio definito
 ♜ l'influenza maggiore è data dal moto di precessione del suo perigeo - a ore 14 della Terra è la parte       più stretta dell'orbita, appunto nei pressi di esso
 ♜ l'attrito di marea allontana la Luna di 3,8 cm/anno, per la 3° legge di Keplero aumenta il suo
      periodo orbitale - tutto cambia, nulla si può ripetere uguale.
 ,

Il moto della Luna é complicato ( ' non complesso ' ) - nella figura due anni terrestri di rivoluzioni del nostro satellite

Parole chiave:
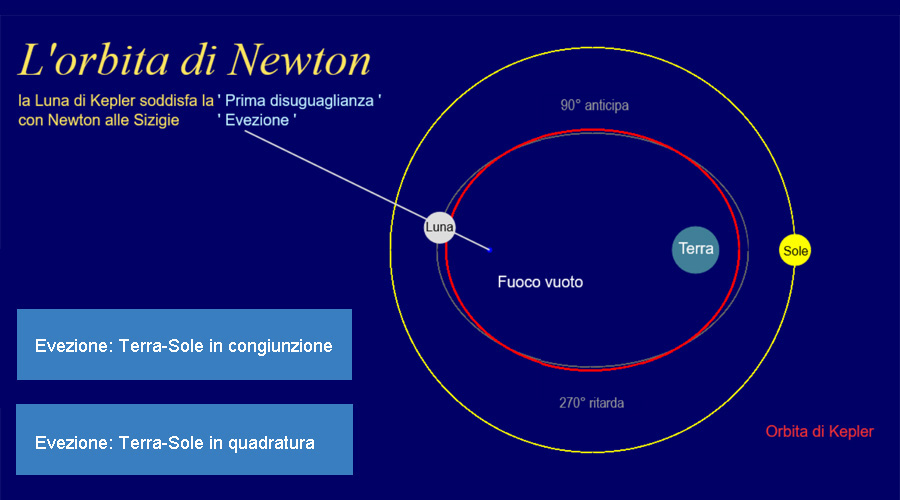
Copernico: modello per il moto lunare
Copernico (1473-1543). La Terra, essendo il corpo centrale, è ferma, attorno ad essa alcuni cerchi:

 ♜ il cerchio blu più grande è fisso e si chiama 'deferente'
 ♜ attorno ad esso ruota un cerchio mezzano, con un segmento orientato in alto, che rende eccentrica
      la Luna rispetto alla Terra: mette in conto il moto non uniforme della Luna - è detto epiciclo
 ♜ il segmento verso l'alto in realtà non è fermo, ma ruota lentamente in senso antiorario: è la
      precessione della linea dei nodi
 ♜ sull'estremo di questo segmento è posizionato il cerchio blu minore, intorno al quale si gira di moto
      antiorario: é l'evezione - anch'esso è detto epiciclo

Questo modello mette in conto tre perturbazioni rispetto al moto circolare uniforme, l'orbita non si richiude come accade nella realtà - un buon modello per l'epoca, con previsioni di longitudine precise entro 30' (il diametro della Luna piena).

È un modello cinematico, cioé riproduce il movimento, non partendo dalle leggi della fisica. La gravitazione sarà una conquista successiva per merito di Newton.

Per effemeridi utili a fare il punto nave bisogna mettere in conto circa 36.000 correzioni.
 ,

Parole chiave:
Newton: moto lunare
Newton (1643-1727) affronta la Luna a partire dalla gravitazione universale. Il suo è il primo attacco scientifico al problema dei tre corpi, che sappiamo non avere una soluzione analitica, ma solo numerica approssimata.

Newton tiene conto dei contributi al moto della Luna di Terra e Sole. Per comprendere come applicare la gravitazione fa riferimento alla geometria tridimensionale delle orbite.

 ♜ l'insieme di queste componenti si traduce in una sorta di geometria differenziale, una branca della
      matematica che nascerà nel '700. Con questo approccio tornano bene la "rotazione dei Nodi",
      la "variazione dell'inclinazione"
 ♜ scopre anche piccole perturbazioni nel moto dei Nodi, nella variazione dell'Eccentricità, che
      vengono a includere quella che storicamente fu l' "Evezione"
 ♜ la precessione del Perigeo ha origini più complicate; non può essere risolta con questo approccio

 ♜ allora, per il moto del Perigeo, Newton introduce termini cinematici, ci lavora in più fasi successive,
      ma i risultati non furono mai soddisfacenti

La teoria della gravitazione universale è valida, e rimarrà non superata fino al 1905 con l'introduzione della relatività ristretta, e nel 1915 di quella generale.
 ,
Eulero: moto lunare
Eulero (1707-83) imposta il calcolo analitico delle pertutbazioni, sia periodiche che secolari.

 ♜ egli affronta con l'analisi matematica il problema dei tre corpi; identifica 2 dei 5 punti di stabilità
      di questa configurazione
 ♜ usa il sistema delle "Coordinate cartesiane"
 ♜ in esse pone le forze come vettori - enti definiti da tre valori - intensità, direzione, verso;
      graficamente possono essere rappresentati con una freccia opportunamente orientata

 ♜ scrive le equazioni di Newton con equazioni differenziali, ottenute a partire dalle leggi della fisica
      e della gravitazione universale
 ♜ dimostra che il problema dei 3 corpi non ha una soluzione analitica
 ♜ studia il problema dei tre corpi ristretto ( nel caso specifico significa trascurare gli influssi
      che la Luna ha verso la Terra e il Sole )
 ♜ sviluppa il calcolo approssimato dei 3 corpi
 ♜ per poter dire in modo quantitativo il moto dei 3 corpi, Eulero deve introdurre le cosiddette
      "condizioni iniziali", nel caso in oggetto 6 valori; esse furono prese dalle osservazioni, ma la
      loro precisione era relativamente modesta, per cui non riuscì pienamente a rispondere alle
      evidenze osservative

 ♜ da questo suo lavoro emerge bene la precessione degli equinozi, la nutazione
 ♜ introduce il concetto di rallentamento planetario, a causa degli attriti mareali

 ♜ calcola la forma del meridiano terrestre, e quindi definisce bene la forma del pianeta Terra;
      il suo studio viene confermato da spedizioni di misura in Lapponia. Questo sarà molto importante
      in futuro per definire nei minimi dettagli il moto lunare
  ,

Parole chiave:
Lagrange: moto lunare
Lagrange (1736-1813), matematico e astronomo, nato a Torino, è attivo prima a Berlino e dopo a Parigi. Nel 1788 scrive la " Mécanique analytique ", sviluppando il " calcolo delle variazioni ".

 ♜ egli affronta il problema dei 3 corpi in modo innovativo, con un orizzonte matematico più ampio
 ♜ abbandona le " forze " di Newton, Eulero, scegliendo nuove variabili, da quelle derivate, che
      includono le reazioni dei vincoli. Questo fa sì che le sue equazioni siano invarianti rispetto al
      sistema di riferimento
 ♜ includono automaticamente le semplificazioni prima cercate con opportuni sistemi di riferimento
      ( es. le semplificazioni in caso di simmetria radiale )

 ♜ lascia dunque le forze, e introduce la " differenza tra energia cinetica e potenziale ".
 ♜ la " lagrangiana " - funzione della nuova variabile lagrangiana, della sua derivata, del tempo - è
      uguale alla differenza T - U ( energia cinetica meno energia potenziale )
 ♜ dalla situazione iniziale a quella finale si può evolvere in molti modi. In assenza di dissipazioni
      ( attrito ), la soluzione è data dal percorso di " minima azione "

Per capire cosa significhi " analisi variazionale ", ecco un esempio: rifrazione della luce che passa da aria a vetro. Calcolo i tempi di percorrenza della luce per tutti i possibili percorsi:


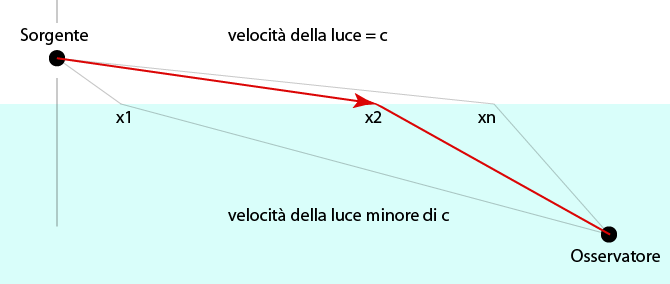
x2 è quello che dà il tempo minimo, è la soluzione: rispetta la rifrazione calcolata con altri metodi.
 ,
Laplace: perturbazioniLaplace (1749-1827), matematico, astronomo, è il massimo scienziato dell'era napoleonica.

 ♜ sviluppa le soluzioni per la meccanica di Newton con i metodi della analisi matematica;
      ne completa e perfeziona alcune parti
 ♜ scrive in 5 volumi la " Traité de Mécanique Céleste " nel periodo 1799-1825
 ♜ questo gli permette di scoprire cose nuove - oltre al moto dei pianeti -, in particolare, tenendo
      conto della influenza dei principali oggetti del Sistema Solare, quantifica la sua
      " teoria delle perturbazioni ", sia periodiche che secolari

 ♜ quantifica il fenomeno della " Accelerazione secolare della Luna ", il conto è
      numericamente abbastanza corretto, ma le ragioni del fenomeno sono errate
 ♜ nella ipotesi di oggetti rigidi, immersi nel vuoto, dimostra che il Sistema Solare è stabile

 ♜ la teoria delle maree è l'applicazione della " meccanica del continuo " per interpretare e
      predire le deformazioni mareali dei corpi planetari, delle loro atmosfere, oceani sotto l'influenza
      gravitazionale di un altro corpo astronomico

 ♜ fonda in matematica la " teoria delle probobilità "; definisce la " Trasformata di Laplace ", che fa
      corrispondere a una funzione di valori reali una di valori complessi; in campo scientifico-tecnologico
      questa trasformazione si rivelerà importantissima
 ♜ su di essa si basano moltissime elaborazioni mediche di immagini; nel campo delle telecomunicazioni
      permette di passare dal segnale microfonico al suo spettro in frequenza, con possibilità di
      filtrare, elaborare, correggere
 ,

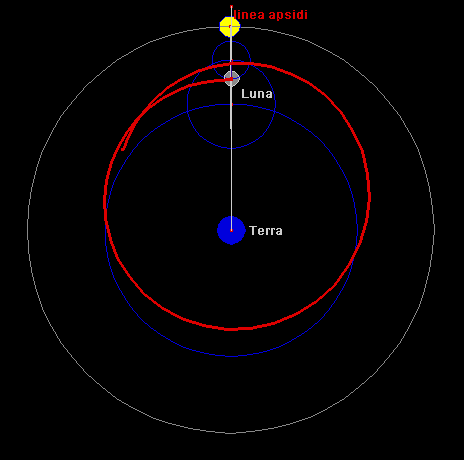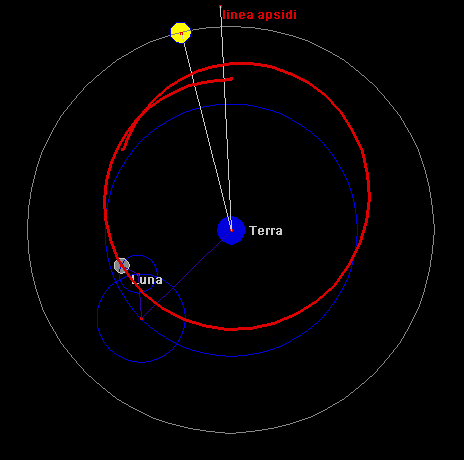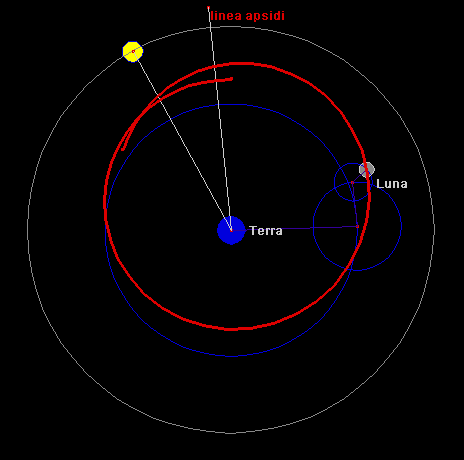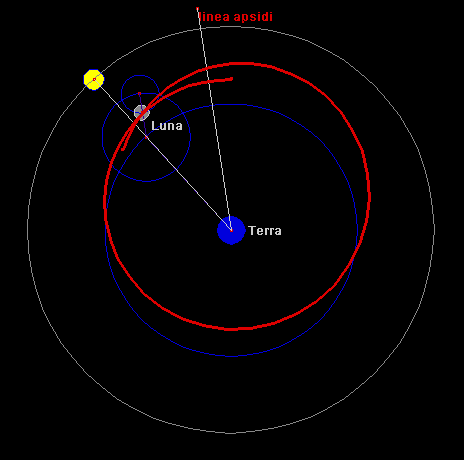
Copernico, con soli tre cerchi, predice la posizione della Luna con una approssimazione di 30 primi

In Geometria un cerchio rotante. Esso si trasforma in Matematica in una funzione seno ( sinusoide )

Disturbi periodici nella longitudine eclittica della Luna

da Moto uniforme a → M' = Anomalia media - max 6,3033° - periodo = T_Anom = 27,5546

• questa Disuguaglianza complessiva era già nota nei fatti agli antichi Greci

Cosa causa le molte altre perturbazioni? - il Sole con le sue forze mareali 

Evezione - max 1,273° - periodo = 31,81 giorni 

• Componente radiale

• ogni Luna nuova o piena

• angolo Luna-Perigeo = Anomalia media
  si corregge col mese Anomalistico