 |
| "Maree"
introduzione ... |
z
In astronomia spesso gli oggetti sono pensati
come masse puntiformi senza dimensioni fisiche.
Questo, evidentemente, non è il caso dei
corpi reali; noi dobbiamo ora considerare gli effetti della applicazione
della gravitazione universale anche alla spazialità che appartiene
ai corpi del Sistema Solare.
Una marea è provocata su un corpo da un
altro a causa degli effetti del "gradiente
gravitazionale" ( variazione nello spazio
del potenziale gravitazionale (1)
) attorno al corpo. Per esempio, se consideriamo
le maree procurate su un pianeta da un satellite orbitante, la forza sperimentata
dalla faccia vicina al satellite è maggiore di quella sperimentata
dalla faccia distante del pianeta.
Poiché nessuno dei corpi del Sistema Solare
è perfettamente rigido, si genera una deformazione che dà
origine ad un "rigonfiamento
mareale".
Come il pianeta subisce una marea da parte del
satellite, così anche il satellite
subisce una marea da parte del pianeta.
Ciò può essere particolarmente importante quando l'orbita
del satellite è eccentrica.
L'ampiezza del
rigonfiamento mareale è determinata
in parte dalla distribuzione interna di densità
e pertanto, spesso, una misura di ampiezza
mareale porta alla determinazione della struttura interna.
Così è stato predetto il vulcanesimo
di Io
- vedi " " "
(1) si ricorda qui che una variazione di
potenziale gravitazionale dà origine a una forza sulla massa presente
in quella zona di spazio
z
Tutto questo saggio, comprese le
formule, è ispirato al libro "Solar
System Dynamics"
di Murray
& Dermott
z |
z
"Maree"
la funzione potenziale ... |
La funzione potenziale
V
è una entità matematica scalare
che esprime l'attitudine a compiere lavoro
...
La forza
F
che agisce su un singolo elemento di sostanza si ottiene dividendo
( meglio derivando
) il potenziale rispetto a una lunghezza
( vettore, perché
segmento orientato ) ...
facile è comprendere quanto descritto ponendo
accanto alla formula il valore dimensionale ( sitema
MKS
)
m
= metro = lunghezza
Kg
= kilogrammo = massa
s = secondo
= tempo
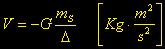 da cui derivando ( dividendo ) per una lunghezza:
da cui derivando ( dividendo ) per una lunghezza: 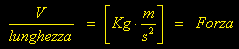
G = costante
gravitazionale
ms
= massa del satellite
D = distanza satellite-pianeta
z |
diventa evidente come sia opportuno
trovare la funzione "potenziale gravitazionale"
attorno ad un pianeta, generata dalle
masse di satellite, pianeta e dalle loro rotazioni ... per semplice derivazione
si otterranno le forze agenti
e quindi con la meccanica e la elasticità le
deformazioni ...
z
"Maree"
la funzione potenziale ... calcolo pratico |
Si parte dalla espressione della funzione potenziale
vista in precedenza: 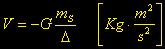
Supponiamo di avere un pianeta di raggio RP,
un satellite S
puntiforme a distanza a,
un punto generico sul pianeta P
a distanza D
come da figura
mediante l'ausilio della trigonometria, segnatamente
il teorema del coseno, ricaviamo D
in funzione di Y
... sarà una funzione trigonometrica ...
z
"Maree"
la funzione potenziale ... calcolo pratico |
z
la relazione tra D
e Y
vale: 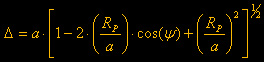
poiché RP<<
a,
si può espandere in modo binomiale ( un
polinomio con potenze di coseno ) e si
ottiene:
la ragione di questo passaggio sta nel fatto
che esso mostra in modo più facilmente comprensibile le tre componenti
più importanti della marea ...
Primo termine :  Secondo termine :
Secondo termine : 
il primo è costante e la sua derivata nulla
non dà forze ... il secondo dà origine alla forza sulla particella
P
necessaria per il moto in un cerchio ... di fatto non contribuisce alla
marea ...
Terzo Termine
:  dove
la funzione P2
vale : dove
la funzione P2
vale : 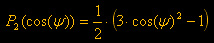
questo è il termine che contiene le principali
componenti di marea ... lo analizzeremo nel dettaglio ...
| z
"Maree"
la funzione potenziale ... calcolo pratico |
Terzo Termine
:  dove
la funzione P2
vale : dove
la funzione P2
vale : 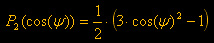
possiamo altresì scrivere :  dove
dove 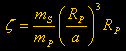 e e 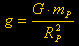 sono costanti note.
sono costanti note.
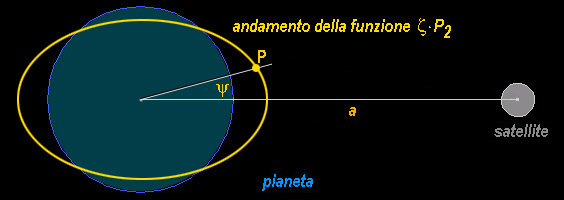
Allora l'andamento del Termine
z ·P2
, che rappresenta la così detta "marea
di equilibrio",
corrisponde all'andamento della marea sul pianeta
z ·P2
presenta un massimo per Y
= 0 e un altro per Y
= p, pertanto
si hanno due bulbi mareali opposti lungo
la direzione Pianeta-Satellite
z ·P2
presenta un minimo per Y
= 1/2 p e un
altro per Y
= 3/2 p, pertanto
si hanno due depressioni alle quadrature
| P2
è una semplificazione ...
ma,
in prima approssimazione,
è soluzione per tutte le situazioni ... |
 |
N.B.
Il doppio bulbo mareale vale per tutti ...
la Luna
sulla Terra
...
Io su Giove
...
la Terra
sulla Luna
...
Giove su
Io ... |
| z
"Maree"
su Terra in moto diurno e ... Luna in moto su orbita inclinata |
Consideriamo la Terra
in rotazione diurna e la Luna
in rivoluzione mensile su un'orbita inclinata
... consideriamo un punto P
sulla Terra
e vediamo di definire geometricamente l'angolo Y
... sostituiremo questa espressione all'interno di P2
...
la relazione vale  ,
la sostituisco in P2
e ottengo : ,
la sostituisco in P2
e ottengo :
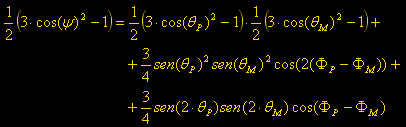 |
z
questo termine ha periodo
....... bi-settimanale
questo termine ha periodo circa
semi-diurno
questo termine ha periodo circa
diurno |
z
"Maree"
su Terra in moto diurno e ... Luna in moto su orbita inclinata |
Analisi del primo termine
: 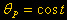 dato che il
punto P è
fisso sulla Terra; dato che il
punto P è
fisso sulla Terra;
vale la trasformazione: una frequenza doppia = alla metà del periodo lunare = periodo
bi-settimanale
una frequenza doppia = alla metà del periodo lunare = periodo
bi-settimanale
Analisi del secondo termine
: ( moto giornaliero molto maggiore
di quello mensile ) = periodo semidiurno ( moto giornaliero molto maggiore
di quello mensile ) = periodo semidiurno
questo periodo è modulato da 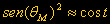 infatti l'angolo varia tra 90° e 85° per cui la funzione varia
tra 1 e 0,9924,
circa costante
infatti l'angolo varia tra 90° e 85° per cui la funzione varia
tra 1 e 0,9924,
circa costante
Analisi del terzo termine
:  ( moto giornaliero molto
maggiore di quello mensile ) = periodo
diurno ( moto giornaliero molto
maggiore di quello mensile ) = periodo
diurno
questo termine è modulato da  che varia tra 0 e 0,1736,
una significativa modulazione bi-settimanale
che varia tra 0 e 0,1736,
una significativa modulazione bi-settimanale
ogni punto P
fisso sulla Terra
è soggetto a queste tre componenti
fondamentali di marea
ci sono altre
componenti minori dovute alla eccentricità
dell'orbita della Luna
... ci sono altre componenti significative dovute alla marea
del Sole.
In particolare vale la seguente relazione quantitativa:
z
 rapporto tra marea Sole
e marea Luna
rapporto tra marea Sole
e marea Luna |
 |
rapporto tra il poteziale
generato dal Sole
e quello prodotto dalla Luna
... ( indotto alla superficie della Terra
) |
|